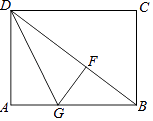
【题目】如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F. 
(1)求证:△ADG≌△FDG;
(2)若BG=2AG,BD=2 ![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】
(1)证明:∵四边形ABCD是矩形,GF⊥BD,
∴∠A=∠DFG=90°,又∠ADG=∠FDG,DG=DG,
在△ADG和△FGD中,
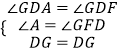 ,
,
∴△ADG≌△FDG.
(2)解:由(1)得△ADG≌△FDG,
∴FG=AG,
∵BG=2AG,
∴BG=2FG,
∴在Rt△BFG中,sin∠FBG= ![]() ,
,
∴∠FBG=30°,
∴AD= ![]() .
.
【解析】(1)根据AAS即可证明△ADG≌△FDG;(2)只要证明∠FBG=30°,即可推出AD= ![]() BD,由此即可解决问题;
BD,由此即可解决问题;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把两个全等的三角板ABC、EFG叠放在一起,使三角板EFG的直角边FG经过三角板ABC的直角顶点C,垂直AB于G,其中∠B=∠F=30°,斜边AB和EF均为4.现将三角板EFG由图1所示的位置绕G点沿逆时针方向旋转α(0°<α<90°),如图2,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题:

(1)求证:△CGH∽△AGK;
(2)连接HK,求证:KH∥EF;
(3)设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.

(1)求证:四边形ABCD是矩形;
(2)若点G为MF的中点,求证:BG是⊙O的切线;
(3)若AD=4,CM=9,求四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=kx+2与x轴、y轴分别交于点A(﹣1,0)和点B,与反比例函数y=
 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n). 
(1)求k的值;
(2)求反比例函数的解析式;
(3)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y= 交于点P、Q,且PQ=2QD,求点D的坐标.
交于点P、Q,且PQ=2QD,求点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AC>BC.
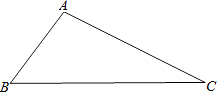
(1)尺规作图:在AC边上求作一点P,使PB=PC(保留作图痕迹,不写作法);
(2)若BC=6,∠C=30°,求△PBC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为9,将正方形折叠,使D点落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是 .

相关试题

