【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
参考答案:
【答案】(1) 5![]() cm;5
cm;5![]() cm;(2) 直线PC与⊙O相切,理由见解析.
cm;(2) 直线PC与⊙O相切,理由见解析.
【解析】
试题分析:(1)连接BD,先求出AC,在Rt△ABC中,运用勾股定理求AC,②由CD平分∠ACB,得出AD=BD,所以Rt△ABD是直角等腰三角形,求出AD,
(2)连接OC,由角的关系求出∠PCB=∠ACO,可得到∠OCP=90°,所以直线PC与⊙O相切.
试题解析:(1)①如图,连接BD,
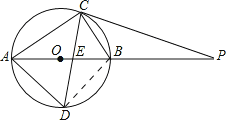
∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
AC=![]() (cm),
(cm),
②∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴![]() ,
,
∴AD=BD,
∴Rt△ABD是直角等腰三角形,
∴AD=![]() AB=
AB=![]() ×10=5
×10=5![]() cm;
cm;
(2)直线PC与⊙O相切,
理由:连接OC,
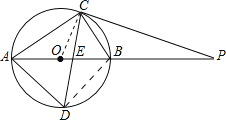
∵OC=OA,
∴∠CAO=∠OCA,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE,
∵CD平分∠ACB,
∴∠ACE=∠ECB,
∴∠PCB=∠CAO=∠ACO,
∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,
即OC⊥PC,
∴直线PC与⊙O相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区改进了用水设施,在5年内小区的居民累计节水39400吨,将39400用科学计数法表示应为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:4ax2﹣4ay2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,若E、F分别是AB、AC上的点,且BE=AF.求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移
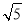 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
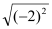 +(﹣1)2016﹣
+(﹣1)2016﹣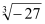
(2)(a4)3(a2)3÷(a4)2
(3)(2x2y﹣x3y2﹣
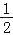 xy3)÷(﹣
xy3)÷(﹣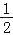 xy)
xy)(4)9(x+2)(x﹣2)﹣(3x﹣1)2
(5)[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x+1>2x-4的解集是( )
A. x<5 B. x>5 C. x<1 D. x>1
相关试题

