【题目】已知△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,若E、F分别是AB、AC上的点,且BE=AF.求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.

参考答案:
【答案】(1)证明过程见解析;(2)证明过程见解析
【解析】试题分析:(1)、题要通过构建全等三角形来求解.连接AD,可通过证△ADF和△BDE全等来求本题的结论.
(2)、与(1)题的思路和解法一样.
试题解析:(1)、连接AD ∵AB=AC,∠A=90°,D为BC中点 ∴AD=![]() =BD=CD
=BD=CD
且AD平分∠BAC ∴∠BAD=∠CAD=45° 在△BDE和△ADF中, ,
,
∴△BDE≌△ADF(SAS) ∴DE=DF,∠BDE=∠ADF ∵∠BDE+∠ADE=90°
∴∠ADF+∠ADE=90° 即:∠EDF=90° ∴△EDF为等腰直角三角形.
(2)、仍为等腰直角三角形. 理由:∵△AFD≌△BED ∴DF=DE,∠ADF=∠BDE
∵∠ADF+∠FDB=90° ∴∠BDE+∠FDB=90° 即:∠EDF=90° ∴△EDF为等腰直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知抛物线y=-x2+4x+5的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.

(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,S△HGF:S△BGF=5:6?
(3)图2所示的抛物线是由y=-x2+4x+5向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区改进了用水设施,在5年内小区的居民累计节水39400吨,将39400用科学计数法表示应为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:4ax2﹣4ay2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移
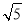 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
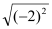 +(﹣1)2016﹣
+(﹣1)2016﹣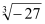
(2)(a4)3(a2)3÷(a4)2
(3)(2x2y﹣x3y2﹣
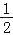 xy3)÷(﹣
xy3)÷(﹣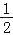 xy)
xy)(4)9(x+2)(x﹣2)﹣(3x﹣1)2
(5)[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x.
相关试题

