搜索
【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（ ）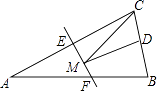
A.6
B.8
C.10
D.12
参考答案：
【答案】C
【解析】解：连接AD，
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC= 
BCAD= ×4×AD=16，解得AD=8，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴AD的长为CM+MD的最小值，
∴△CDM的周长最短=（CM+MD）+CD=AD+ BC=8+ ×4=8+2=10．
故选C．
【考点精析】根据题目的已知条件，利用轴对称-最短路线问题的相关知识可以得到问题的答案，需要掌握已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知同一平面上的两个角的两条边分别平行，则这两个角（ ）
A. 相等 B. 互补 C. 相等或互补 D. 不能确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知Rt△ABC中，∠B=90°，AC=20，AB=10，P是边AC上一点（不包括端点A、C），过点P作PE⊥BC于点E，过点E作EF∥AC，交AB于点F．设PC=x，PE=y．
（1）求y与x的函数关系式；
（2）是否存在点P使△PEF是Rt△？若存在，求此时的x的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2，b1≠b2，那么称这两个一次函数为“平行一次函数”．如图，已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点，一次函数y=kx+b与y=﹣2x+4是“平行一次函数”．
（1）若函数y=kx+b的图象过点（3，1），求b的值；
（2）若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形，位似中心为原点，位似比为1：2，求函数y=kx+b的表达式．
-
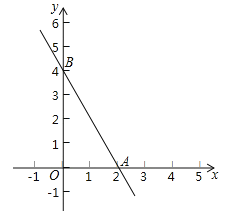
科目： 来源： 题型：
查看答案和解析>>【题目】如果∠α和∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③
（∠α+∠β）；④ （∠α﹣∠β）．正确的有（ ）
A.4个
B.3个
C.2个
D.1个 -
科目： 来源： 题型：
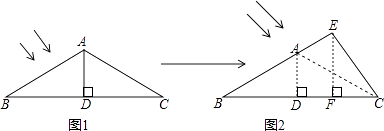
查看答案和解析>>【题目】如图1，某温室屋顶结构外框为△ABC，立柱AD垂直平分横梁BC，∠B=30°，斜梁AC=4m，为增大向阳面的面积，将立柱AD增高并改变位置后变为EF，使屋顶结构外框由△ABC变为△EBC（点E在BA的延长线上）如图2所示，且立柱EF⊥BC，若EF=3m，则斜梁增加部分AE的长为m．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校、乙同学骑自行车去学校．已知甲步行速度是乙骑自行车速度的
，公交车的速度是乙骑自行车速度的2倍．甲乙两同学同时从家发去学校，结果甲同学比乙同学早到2分钟．
（1）求乙骑自行车的速度；
（2）当甲到达学校时，乙同学离学校还有多远？
相关试题
