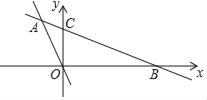
【题目】如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于点B、C,与直线OA交于点A.已知点A的坐标为(﹣3,5),OC=4.
(1)分别求出直线AB、AO的解析式;
(2)求△ABO的面积.
参考答案:
【答案】(1)直线AB的解析式为y=﹣![]() x+4,直线AO的解析式为y
x+4,直线AO的解析式为y![]() x;(2)30.
x;(2)30.
【解析】
(1)由点A的坐标,利用待定系数法可求出直线AO的解析式,由OC及点C的位置可得出点C的坐标,结合点A的坐标,利用待定系数法即可求出直线AB的解析式;
(2)利用一次函数图象上点的坐标特征可求出OB的长度,过点A作AD⊥x轴于点D,由点A的坐标可得出AD的长度,再利用三角形的面积公式即可求出△ABO的面积.
设直线AO的解析式为y=kx(k≠0),
将A(﹣3,5)代入y=kx,得:5=﹣3k,解得:k![]() ,
,
∴直线AO的解析式为y![]() x.
x.
∵OC=4,点C在y轴正半轴,
∴点C的坐标为(0,4).
设直线AB的解析式为y=mx+n(m≠0),
将A(﹣3,5),C(0,4)代入y=mx+n,得:![]() ,
,
解得: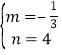 ,
,
∴直线AB的解析式为y![]() x+4.
x+4.
当y=0时,![]() x+4=0,解得:x=12,
x+4=0,解得:x=12,
∴OB=12.
过点A作AD⊥x轴于点D,如图所示.
∵点A的坐标为(﹣3,5),
∴AD=5,
∴S△AOB![]() OBAD
OBAD![]() 12×5=30.
12×5=30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某经销商从市场得知如下信息:
A品牌计算器
B品牌计算器
进价(元/台)
700
100
售价(元/台)
900
160
他计划用不超过4万元的资金一次性购进这两种品牌计算器共100台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?
(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:
 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2: 交于点A.
交于点A.(1)求出点A的坐标
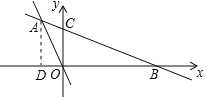
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车和一辆快车沿相同的路线从A地到B地,所行驶的路程与时间的函数图形如图所示,下列说法正确的有( )
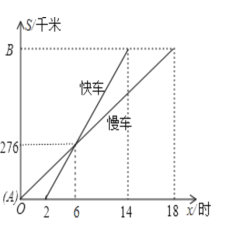
①快车追上慢车需6小时;②慢车比快车早出发2小时;③快车速度为46km/h;④慢车速度为46km/h; ⑤A、B两地相距828km;⑥快车从A地出发到B地用了14小时
A. 2个B. 3个C. 4个D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在互联网技术的影响下,幸福新村的村民小刘在网上销售苹果,原计划每天卖100千克,但实际每天的销量与计划销量相比有出入,如表是某周的销售情况(超额记为正,不足记为负.单位:千克):
星期
一
二
三
四
五
六
日
与计划量的差值
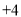
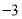
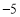
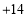
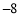
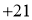
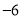
(1)根据表中的数据可知前三天共卖出___________千克;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售多少千克?
(3)若每千克按5元出售,每千克苹果的运费为1元,那么小刘本周一共收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,AE
中,AE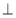 BC于点E,延长BC至点F,点使
BC于点E,延长BC至点F,点使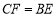 ,连接AF、DE、DF。
,连接AF、DE、DF。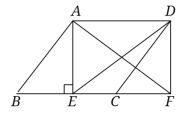
(1)求证:四边形AEFD是矩形;
(2)若
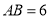 ,
,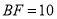 ,,求AE的长。
,,求AE的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】实验中学地理社团学生在5名地理老师的带领下去黄河风景区进行参观考察,景区的门票为每人40元.现有两种优惠方案.甲方案:带队教师免费,学生按9折收费;乙方案:师生都8折收费.
(1)若有
 名学生,用代数式表示两种优惠方案各需多少元?
名学生,用代数式表示两种优惠方案各需多少元?(2)当
 为何值时,两种优惠方案收费相同?
为何值时,两种优惠方案收费相同?(3)当
 时,采用哪种方案优惠?
时,采用哪种方案优惠?
相关试题

