【题目】某经销商从市场得知如下信息:
A品牌计算器 | B品牌计算器 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他计划用不超过4万元的资金一次性购进这两种品牌计算器共100台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?
(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?
参考答案:
【答案】(1) ![]() ;(2) 三种进货方案,详见解析;(3)选择方案③进货时,经销商可获利最大,最大利润是13000元
;(2) 三种进货方案,详见解析;(3)选择方案③进货时,经销商可获利最大,最大利润是13000元
【解析】
(1)根据总利润=单块利润×购进数量,即可得出y关于x的函数关系式;
(2)根据总价=单价×购进数量结合(1)的结论,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,取其整数值即可得出各进货方案;
(3)由(1)的结论,利用一次函数的性质即可解决最值问题.
解:(1) ![]()
![]() ,
,
其中![]() ,得
,得![]() ,
,
即![]() ;
;
(2)令![]() ,则
,则![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
![]() 为整数
为整数
![]() 经销商有以下三种进货方案:
经销商有以下三种进货方案:
方案 |
|
|
① | 48 | 52 |
② | 49 | 51 |
③ | 50 | 50 |
(3) ![]() ,
,
![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 时,
时,![]() 取得最大值,
取得最大值,
又![]() ,
,
![]() 选择方案③进货时,经销商可获利最大,最大利润是13000元。
选择方案③进货时,经销商可获利最大,最大利润是13000元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
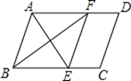
A. 13B. 14C. 15D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
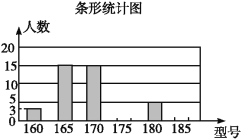
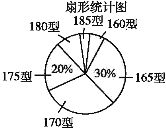
根据以上信息,解答下列问题:
(1)该班共有 名学生?其中穿175型校服的学生有 人.
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角度数为 ;
(4)该班学生所穿校服型号的众数是 ,中位数是 .
-
科目: 来源: 题型:
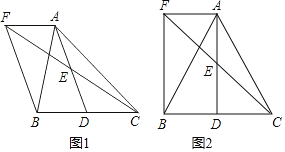
查看答案和解析>>【题目】如图1,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:点D是线段BC的中点;
(2)如图2,若AB=AC=13,AF=BD=5,求四边形AFBD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:
 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2: 交于点A.
交于点A.(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车和一辆快车沿相同的路线从A地到B地,所行驶的路程与时间的函数图形如图所示,下列说法正确的有( )
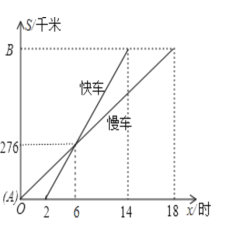
①快车追上慢车需6小时;②慢车比快车早出发2小时;③快车速度为46km/h;④慢车速度为46km/h; ⑤A、B两地相距828km;⑥快车从A地出发到B地用了14小时
A. 2个B. 3个C. 4个D. 5个
-
科目: 来源: 题型:
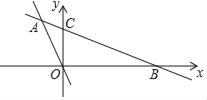
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于点B、C,与直线OA交于点A.已知点A的坐标为(﹣3,5),OC=4.
(1)分别求出直线AB、AO的解析式;
(2)求△ABO的面积.
相关试题

