【题目】如图1,现有一个长方体水槽放在桌面上,从水槽内量得它的侧面高20cm,底面的长25cm,宽20cm,水槽内水的高度为acm,往水槽里放入棱长为10cm的立方体铁块.
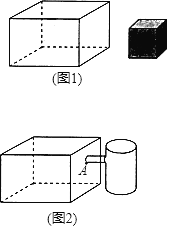
(1)求下列两种情况下a的值.
①若放入铁块后水面恰好在铁块的上表面;
②若放入铁块后水槽恰好盛满(无溢出).
(2)若0<a≤18,求放入铁块后水槽内水面的高度(用含a的代数式表示).
(3)如图2,在水槽旁用管子连通一个底面在桌面上的圆柱形容器,内部底面积为50cm2,管口底部A离水槽内底面的高度为hcm(h>a),水槽内放入铁块,水溢入圆柱形容器后,容器内水面与水槽内水面的高度差为8.2cm,若a=15,求h的值.(水槽和容器的壁及底面厚度相同)
参考答案:
【答案】(1)①a=8;②a=18;(2)1.25a或a+2;(3)h=16.2.
【解析】
(1)①根据题意列出方程得出a的值即可;②根据题意列出方程得出a的值即可;(2)设放入铁块后水槽内水面的高度为xcm,根据题意列出方程解答即可;(3)根据题意得出方程解答即可.
(1)①由题意得:25×20×a=25×20×10-103,
解得:a=8,
②25×20×20=103+25×20×a,
解得:a=18,
(2)设放入铁块后水槽内水面的高度为xcm,
当0<a≤8时,由题意得:25×20x=10×10x+25×20×a,
解得:x=1.25a,
当8<a≤18时,由题意得:25×20x=103+25×20×a,
解得:x=a+2;
(3)由题意得:50(h-8.2)=500(15+2-h)
解得:h=16.2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动问题情境:
如图1,在△ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将△ADE绕点A顺时针旋转α角(0°<α<90°)得到△AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
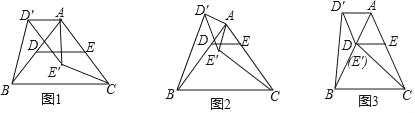
探究发展:
(1)图1中,猜想CE′与BD′的数量关系,并证明;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E“,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在△ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将△ADE绕点A顺时针旋转60°得到△AD′E′,连接CE′,BD′,请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:

(1)用一种正多边形镶嵌平面
例如,用 6 个全等的正三角形镶嵌平面,摆放方案如图所示:
若用 m 个全等的正 n 边形镶嵌平面,求出 m,n 应满足的关系式;
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案;
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有 n 个,设这 n 个正多边形的边数分别为 x1,x2,…,xn,求出 x1,x2,…,xn 应满足的关系式.(用含 n 的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
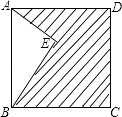
A.48
B.60
C.76
D.80 -
科目: 来源: 题型:
查看答案和解析>>【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
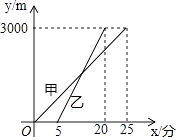
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米? -
科目: 来源: 题型:
查看答案和解析>>【题目】把(sinα)2记作sin2α,根据图1和图2完成下列各题.
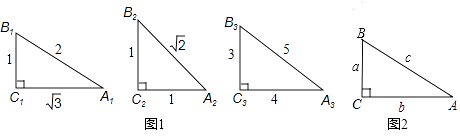
(1)sin2A1+cos2A1= , sin2A2+cos2A2= , sin2A3+cos2A3=;
(2)观察上述等式猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A=;
(3)如图2,在Rt△ABC中证明(2)题中的猜想:
(4)已知在△ABC中,∠A+∠B=90°,且sinA=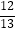 ,求cosA.
,求cosA.
相关试题

