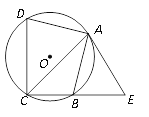
【题目】如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=![]() ,tan∠ADC=3,求BE的长.
,tan∠ADC=3,求BE的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OA、OB,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)过点A作AF⊥CD于点F,由AB=AD,得到∠ACD=∠ACB=45°,在Rt△AFC中可求得AF=3,在Rt△AFD中求得DF=1,所以AB=![]() =
=![]() ,CD= CF+DF=4,再证明△ABE∽△CDA,得出
,CD= CF+DF=4,再证明△ABE∽△CDA,得出![]() ,即可求出BE的长度;
,即可求出BE的长度;
试题解析:
(1)证明:连结OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB= 90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点A作AF⊥CD于点F,则∠AFC=∠AFD=90°.
∵AB=AD,
∴![]() =
=![]()
∴∠ACD=∠ACB=45°,
在Rt△AFC中,
∵AC=![]() ,∠ACF=45°,
,∠ACF=45°,
∴AF=CF=AC·sin∠ACF =3,
∵在Rt△AFD中, tan∠ADC=![]() ,
,
∴DF=1,
∴![]() ,
,
且CD= CF+DF=4,
∵四边形ABCD内接于⊙O,
∴∠ABE=∠CDA,
∵∠BAE=∠DCA,
∴△ABE∽△CDA,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.

(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的一条边AD=8 cm,点P在CD边上,AP=AB, PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.
(1)求AB的长;
(2)若点M的运动速度为1cm/s,点N的运动速度为2cm/s,△AMN的面积为S,点M和点N的运动时间为
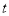 ,求S与
,求S与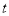 的函数关系式,并求S的最大值;
的函数关系式,并求S的最大值;(3)若点M和点N的运动速度相等,作ME⊥BP于点E.试问当点M、N在运动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
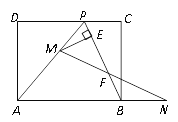
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程(a+1)x2+2x﹣1=0是一元二次方程,则a的取值范围是( )
A.a≠﹣1B.a>﹣1C.a<﹣1D.a≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】荔枝是岭南一带的特色时令水果.今年5月份荔枝一上市,某水果店的老板用3000元购进了一批荔枝,由于荔枝刚在果园采摘比较新鲜,前两天他以高于进价40% 的价格共卖出150千克,由于荔枝保鲜期短,第三天他发现店里的荔枝卖相已不大好,于是果断地将剩余荔枝以低于进价20%的价格全部售出,前后一共获利750元.
(1)若购进的荔枝为
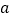 千克,则这批荔枝的进货价为 ;(用含
千克,则这批荔枝的进货价为 ;(用含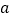 的式子来表示)
的式子来表示)(2)求该水果店的老板这次购进荔枝多少千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强环境保护意识,6月5日“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),将调查的数据进行处理(设所测数据是正整数),得不完整频数分布表和频数分布直方图如下:
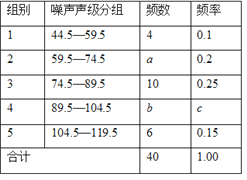
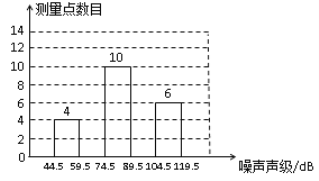
根据表中提供的信息解答下列问题:
(1)频数分布表中的a =________,b=________,c =_________;
(2)请补全频数分布直方图;
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面各组数中,相等的一组是( )
A.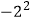 与
与 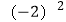
B.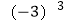 与
与 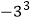
C.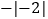 与
与 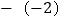
D.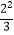 与
与 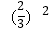
相关试题

