【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC; ②四边形ADFE为菱形; ③AD=4AG; ④FH=![]() BD
BD
其中正确的结论有( ).

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
参考答案:
【答案】C
【解析】∵△ACE是等边三角形,∴∠EAC=60°,AE=AC.
∵∠BAC=30°,∴∠FAE=∠ACB=90°,AB=2BC.
∵F为AB的中点,∴AB=2AF,∴BC=AF,∴△ABC≌△EFA,∴FE=AB,
∴∠AEF=∠BAC=30°,∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,∴HF∥BC.
∵F是AB的中点, ![]() .
.
![]() ,AB=BD,
,AB=BD, ![]() ,故④说法正确;
,故④说法正确;
∵AD=BD,BF=AF,∴∠DFB=90°,∠BDF=30°.
∵∠FAE=∠BAC+∠CAE=90°,∴∠DFB=∠EAF.
∵EF⊥AC,∴∠AEF=30°,∴∠BDF=∠AEF,∴△DBF≌△EFA(AAS),∴AE=DF.
∵FE=AB,∴四边形ADFE为平行四边形.
∵AE≠EF,∴四边形ADFE不是菱形;故②说法不正确;
∵四边形ADFE为平行四边形,
![]() ,
, ![]() .
.
∵AD=AB,∴AD=4AG,故③说法正确,
所以正确的有:①③④.故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正比例函数经过点(-1,2),该函数解析式为________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并讨论.

已知ΔABC,如图所示,要求画一个三角形,使它与ΔABC有一个公共的顶点C,并且与ΔABC全等。
甲同学的画法如下:
①延长BC和AC;
②在BC的延长线上取点D,使CD=BC;
③在AC的延长线上取点E,使CE=AC;
④连接DE,得ΔEDC.
乙同学的画法如下:
①延长AC和BC;
②在BC的延长线上取点M,使CM=AC;
③在AC的延长线上取点N,使CN=BC;
④连接MN,得ΔMNC.
究竟哪种画法对?有如下几种结论:
A.甲画得对,乙画得不对; B. 乙画得对,甲画得不对;
C.甲、乙画得都对; D.甲、乙画得都不对.
正确的结论是 .
这道题还可以按下面步骤完成:
①用量角器量出∠ACB的度数;
②在∠ACB的外部画射线CP,使∠ACP=∠ACB;
③在射线CP上取点D,使CD=CB;
④连接AD.
ΔADC就是所要画的三角形.
这样画的结果可记作ΔABC≌ .
满足题目要求的三角形可以画出多少个呢?
答案是 .请你再设计一种画法并画出图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并完成填空.
你能比较20152 016和20162 015的大小吗?
为了解决这个问题,先把问题一般化,比较nn+1和(n+1)n(n≥1,且n为整数)的大小.然后从分析n=1,n=2,n=3…的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
(1)通过计算(可用计算器)比较下列①~⑦组两数的大小:(在横线上填上“>”“=”或“<”)
①12____21;②23_____32;③34_____43;④45_____54;
⑤56____65;⑥67_____76;⑦78_____87;
(2)归纳第(1)问的结果,可以猜想出nn+1和(n+1)n的大小关系;
(3)根据以上结论,可以得出20162017和20172016的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四种沿
 折叠的方法中,不一定能判定纸带两条边线
折叠的方法中,不一定能判定纸带两条边线 ,
,  互相平行的是( ).
互相平行的是( ).
A. 如图
 ,展开后测得
,展开后测得
B. 如图
 ,展开后测得
,展开后测得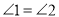
C. 如图
 ,测得
,测得
D. 如图
 ,展开后再沿
,展开后再沿 折叠,两条折痕的交点为
折叠,两条折痕的交点为 ,测得
,测得 ,
, 
-
科目: 来源: 题型:
查看答案和解析>>【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:9x2y﹣y=_____.
相关试题

