【题目】阅读
(1)阅读理解: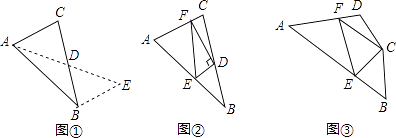
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
参考答案:
【答案】
(1)2<AD<8
(2)
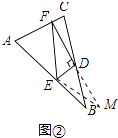
解:证明:延长FD至点M,使DM=DF,连接BM,EM,如图②所示:
同(1)得:△BMD≌△CFD(SAS),
∴BM=CF,
∵DE⊥DF,DM=DF,
∴EM=EF,
在△BME中,由三角形的三边关系得:BE+BM>EM,
∴BE+CF>EF
(3)
解:BE+DF=EF;理由如下:
延长AB至点N,使BN=DF,连接CN,如图3所示:
∵∠ABC+∠D=180°,∠NBC+∠ABC=180°,
∴∠NBC=∠D,
在△NBC和△FDC中, 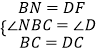 ,
,
∴△NBC≌△FDC(SAS),
∴CN=CF,∠NCB=∠FCD,
∵∠BCD=140°,∠ECF=70°,
∴∠BCE+∠FCD=70°,
∴∠ECN=70°=∠ECF,
在△NCE和△FCE中, 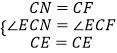 ,
,
∴△NCE≌△FCE(SAS),
∴EN=EF,
∵BE+BN=EN,
∴BE+DF=EF

【解析】(1)解:延长AD至E,使DE=AD,连接BE,如图①所示:
∵AD是BC边上的中线,
∴BD=CD,
在△BDE和△CDA中,  ,
,
∴△BDE≌△CDA(SAS),
∴BE=AC=6,
在△ABE中,由三角形的三边关系得:AB﹣BE<AE<AB+BE,
∴10﹣6<AE<10+6,即4<AE<16,
∴2<AD<8;
所以答案是:2<AD<8;
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我省为135万名农村中小学生免费提供教科书,减轻了农民的负担135万用科学记数法可表示为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥OD,∠BOC比∠DOC大34°,OE平分∠AOC,求:
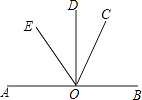
(1)∠COD的大小;
(2)∠DOE的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x﹣3的图象与x轴交点的坐标是 , y轴的交点坐标是 , 顶点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b(kb<0)图象一定经过第__________ 象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(1)a(1-a)+(a+1)2-1;
(2)(x-y)2-(x-2y)(x+y).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)某班“2011年新春联欢会”中,有一个摸奖游戏,规则如下:有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、 2张哭脸.现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现小芳有一次翻牌机会,若正面是笑脸的就获奖,正面是哭脸的不获奖.她从中随机翻开一张纸牌,小芳获奖的概率是 .
(2)如果小芳、小明都有翻两张牌的机会.小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.他们获奖的机会相等吗?请说明理由.
相关试题

