【题目】如图,在△ABC 中,AB=AD,CB=CE.
(1)当∠ABC=90°时(如图①),∠EBD= °;
(2)当∠ABC=n°(n≠90)时(如图②),求∠EBD 的度数(用含 n 的式子表示).

参考答案:
【答案】(1)45;(2) ∠DBE=90°-![]() n°.
n°.
【解析】
(1)根据等腰三角形的性质,即可得到∠ABD=∠ADB=![]() (180°-∠A),∠CBE=∠CEB=
(180°-∠A),∠CBE=∠CEB=![]() (180°-∠C),再根据三角形内角和定理,即可得到∠DBE的度数;
(180°-∠C),再根据三角形内角和定理,即可得到∠DBE的度数;
(2)运用(1)中的方法进行计算,即可得到∠EBD的度数.
解:(1)∵AB=AD,CB=CE,
∴∠ABD=∠ADB=![]() (180°-∠A),∠CBE=∠CEB=
(180°-∠A),∠CBE=∠CEB=![]() (180°-∠C),
(180°-∠C),
∵∠ABC=90°,
∴∠A+∠C=90°,
∴△BDE中,∠DBE=180°-(∠ADB+∠CEB)
=180°-![]() (180°-∠A)-
(180°-∠A)-![]() (180°-∠C)
(180°-∠C)
=![]() (∠A+∠C)
(∠A+∠C)
=![]() ×90°
×90°
=45°,
故答案为:45.
(2)∵AB=AD,CB=CE,
∴∠ABD=∠ADB=![]() (180°-∠A),∠CBE=∠CEB=
(180°-∠A),∠CBE=∠CEB=![]() (180°-∠C),
(180°-∠C),
∵∠ABC=n°,
∴∠A+∠C=180°-n°,
∴△BDE中,∠DBE=180°-(∠ADB+∠CEB)
=180°-![]() (180°-∠A)-
(180°-∠A)-![]() (180°-∠C)
(180°-∠C)
=![]() (∠A+∠C)=
(∠A+∠C)=![]() ×(180°-n°)
×(180°-n°)
=90°-![]() n°.
n°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程
 的解为
的解为 ,不等式组
,不等式组 的解集为
的解集为 ,因为
,因为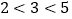 ,所以,称方程
,所以,称方程 为不等式组
为不等式组 的关联方程.
的关联方程.(1)在方程①
 ,②
,② ,③
,③ 中,不等式组
中,不等式组 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)(2)若不等式组
 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)(3)若方程
 ,
, 都是关于
都是关于 的不等式组
的不等式组 的关联方程,求
的关联方程,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心都在原点,且各边也都与x轴或y轴平行,从内向外,它们的边长依次为2,4,6,8,…顶点依次用A1、A2、A3、A4表示,则顶点A2020的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图,并且C的对应点C′的坐标为(4,1)。
(1)A′、B′.两点的坐标分别为A′ 、B′ ;
(2)请作出△ABC平移之后的图形△A′B′C′;
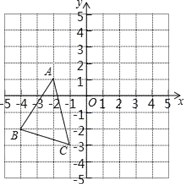
(3)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )
A.平均数是1
B.众数是-1
C.中位数是0.5
D.方差是3.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 与x轴和 y 轴分别交与A,B 两点,另一直线经过点B和点C(6,-5).
与x轴和 y 轴分别交与A,B 两点,另一直线经过点B和点C(6,-5).(1)求 A,B 两点的坐标;
(2)证明:△ABC 是直角三角形;
(3)在 x 轴上找一点 P,使△BCP 是以 BC 为底边的等腰三角形,求出 P 点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
相关试题

