【题目】已知直线![]() 与x轴和 y 轴分别交与A,B 两点,另一直线经过点B和点C(6,-5).
与x轴和 y 轴分别交与A,B 两点,另一直线经过点B和点C(6,-5).
(1)求 A,B 两点的坐标;
(2)证明:△ABC 是直角三角形;
(3)在 x 轴上找一点 P,使△BCP 是以 BC 为底边的等腰三角形,求出 P 点坐标.

参考答案:
【答案】(1) A(-4,0),B(0,3);(2)见解析;(3) P(![]() ,0).
,0).
【解析】
(1)由直线解析式求出A与B坐标即可;
(2)由B与C的坐标确定出直线BC的斜率,由已知AB的斜率,得到两直线斜率乘积为-1,可得AB与BC垂直,即可得证;
(3)作出线段BC的垂直平分线,与x轴交于点P,与直线BC交于点Q,利用中点坐标公式求出Q的坐标,根据PQ与AB都与BC垂直,得到PQ与AB平行,即斜率相等,求出直线PQ解析式,进而求出P坐标.
解:(1)对于直线y=![]() x+3,
x+3,
令x=0,得到y=3;令y=0,得到x=-4,
则A(-4,0),B(0,3);
(2)由B(0,3),C(6,-5),得到直线BC斜率为![]() =-
=-![]() ,
,
∵直线AB斜率为![]() ,
,
∴直线AB与直线BC斜率乘积为-![]() ×
×![]() =-1,
=-1,
∴AB⊥BC,
则△ABC是直角三角形;
(3)如图所示,作出BC的垂直平分线PQ,与x轴交于点P,与直线BC交于点Q,连接BP,CP,
则△BCP是以BC为底边的等腰三角形,
∵PQ⊥BC,AB⊥PQ,
∴PQ∥AB,即直线PQ与直线AB斜率相同,即为![]() ,
,
∵B(0,3),C(6,-5),
∴线段BC中点Q坐标为(3,-1),
∴直线PQ解析式为y+1=![]() (x-3),即y=
(x-3),即y=![]() x-
x-![]() ,
,
令y=0,得到x=![]() ,
,
则点P(![]() ,0).
,0).
-
科目: 来源: 题型:
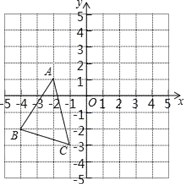
查看答案和解析>>【题目】如图所示,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图,并且C的对应点C′的坐标为(4,1)。
(1)A′、B′.两点的坐标分别为A′ 、B′ ;
(2)请作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AD,CB=CE.
(1)当∠ABC=90°时(如图①),∠EBD= °;
(2)当∠ABC=n°(n≠90)时(如图②),求∠EBD 的度数(用含 n 的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )
A.平均数是1
B.众数是-1
C.中位数是0.5
D.方差是3.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为践行“绿水青山就是金山银山”的理念,坚持绿色发展,建设美丽家园,青年大学生小王准备在家乡边疆种植两种树木.经研究发现,A种树木种植费用y(元)与 种植面积 x(m2)的函数表达式如图所示,B种树木的种植费用为400元/ m2.
(1)求y与x的函数表达式;
(2)A种树木和 B 种树木种植面积共 1500 m,若A种树木种植面积不超过B种树木种 植面积的2倍,且 A 种树木种植面积不少于 400 m,应该如何分配A种树木和B种树木的种植面积才能使得总费用最少?最少费用是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工地因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
租金(单位:元/台时)
挖掘土石方量(单位:m3/台时)
甲型机
100
60
乙型机
120
80
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
相关试题

