【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的长方形花圃.

(1)设花圃的一边AB为xm,则BC的长可用含x的代数式表示为______m;
(2)当AB的长是多少米时,围成的花圃面积为63平方米?
参考答案:
【答案】(1)30-3x;(2)7
【解析】
(1)由AB的长为xm,结合长为30m的篱笆即可表示出BC的长为:(30﹣3x)m;
(2)根据AB及BC的长可表示出花圃的面积,令该面积等于63,求出符合题意的x的值,即是所求AB的长.
解:(1)由题意得:BC=30﹣3x,
故答案为:30﹣3x;
(2)由题意得:﹣3x2+30x=63.
解此方程得x1=7,x2=3.
当x=7时,30﹣3x=9<10,符合题意;
当x=3时,30﹣3x=21>10,不符合题意,舍去;
故当AB的长为7m时,花圃的面积为63m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动 实验、猜想与证明
问题情境
(1)数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.

解决问题
(2)小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(3)小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知A(a,b),且a.b满足
 ,
,(1)求A点的坐标及线段OA的长度;(2)点P为x轴正半轴上一点,且△AOP是等腰三角形,求P点的坐标;
(3)如图2,若B(1,0),C(0,-3),试确定∠ACO+∠BCO的值是否发生变化,若不变,求其值;若变化,请求出变化范围。


-
科目: 来源: 题型:
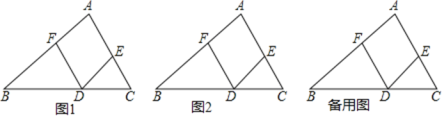
查看答案和解析>>【题目】已知:如图1,DE∥AB,DF∥AC.
(1)求证:∠A=∠EDF.
(2)点G是线段AC上的一点,连接FG,DG.
①若点G是线段AE的中点,请你在图2中补全图形,判断∠AFG,∠EDG,∠DGF之间的数量关系,并证明.
②若点G是线段EC上的一点,请你直接写出∠AFG,∠EDG,∠DGF之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:

根据以上图表信息,解答下列问题:
(1)表中的a= ,m= ;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数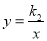 的图象相交于
的图象相交于 、
、 两点,其中点
两点,其中点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 .
.
(1)根据图象,直接写出满足
 的
的 的取值范围;
的取值范围;(2)求这两个函数的表达式;
(3)点
 在线段
在线段 上,且
上,且 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
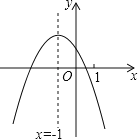
A. 4个 B. 3个 C. 2个 D. 1个
相关试题

