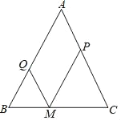
【题目】已知:在△ABC中,AB=AC=5,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
(1)求四边形AQMP的周长;
(2)M位于BC的什么位置时,四边形AQMP为菱形?指出点M的位置,并加以证明.
参考答案:
【答案】(1)四边形AQMP的周长=10;(2)点M位于BC的中点时,四边形AQMP是菱形.理由见解析.
【解析】
(1)根据有两组对边分别平行的四边形是平行四边形证明即可;
(1)根据平行四边形的性质可得到对应角相等对应边相等,从而不难求得其周长.
(1)∵AB∥MP,QM∥AC,∴四边形APMQ是平行四边形,∴AQ=MP,QM=AP.
∵AB=AC,∴∠B=∠C.
∵∠B=∠PMC,∠C=∠QMB,∴∠PMC=∠QMB,∴BQ=QM,PM=PC,∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=10.
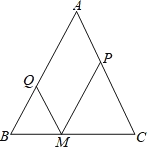
(2)点M位于BC的中点时,四边形AQMP是菱形.理由如下:
∵BM=MC,PM∥AB,MQ∥AC,∴AP=PC,AQ=BQ,∴PM![]() AB,MQ
AB,MQ![]() AC.
AC.
∵AB=AC,∴MP=MQ.
∵四边形AQMP是平行四边形,∴四边形AQMP是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3cm,动点P从点A出发,沿AB方向以每秒2cm的速度向终点B运动;同时,动点Q从点B出发沿BC力向以每秒1cm的速度向终点C运动,将△PQC翻折,点P的对应点为R,设点Q运动的时间为t秒,若四边形PCRQ为菱形,则t的值为( )

A.
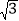 B. 2C. 1D.
B. 2C. 1D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在某一次实验中,测得两个变量之间的关系如下表所示:
自变量x
1
2
3
4
12
因变量y
12.03
5.98
3.04
1.99
1.00
请你根据表格回答下列问题:
① 这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由。
②请你写出这个函数的解析式。
③表格中空缺的数值可能是多少?请你给出合理的数值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场出售一批进价为2元的贺卡,在市场营销中发现商品的日销售单价x元与日销售量y个之间有如下关系:
x(元/个)
3
4
5
6
y(个)
20
15
12
10
(1)根据表中数据,在直角坐标系描出实数对(x,y)的对应点
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为W元,试求出W与x之间的函数关系式,若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋中装有9个黄球,13个黑球,11个红球,它们除颜色外其余都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取出若干个黄球,井放入相同数量的黑球,若要使搅拌均与后从袋中摸出一个球是黑球的概率不小于
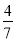 ,问至少要取出多少个黄球?
,问至少要取出多少个黄球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,D、F分别为BC、AB边上的点,AF=BD,以AD为边作等边ΔADE.
(1)求证:AE=CF;
(2)求∠BEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
请你回答:AP的最大值是 .
参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是 .(结果可以不化简)

相关试题

