【题目】如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE.
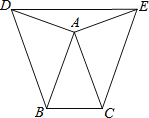
(1)求证:AB=AC;
(2)若∠DAE=2∠ABC=140°,求∠BAD的度数.
参考答案:
【答案】(1)证明见解析(2)90°
【解析】
试题分析:(1)由等腰三角形的性质可知∠ADE=∠AED,从而可得到∠ADB=∠AEC,依据AAS可证明△ADB≌△AEC;
(2)由题意可知:∠ABC=70°,由等腰三角形的性质可知∠ABC=∠ACB=70°,由三角形内角和定理可知∠BAC=40°,由△ADB≌△AEC可知∠DAB=∠EAC,故此∠BAD=![]() (360°﹣140°﹣40°)=90°.
(360°﹣140°﹣40°)=90°.
(1)证明:∵AD=AE,
∴∠ADE=∠AED.
∵∠BDE=∠CED,
∴∠BDE﹣∠ADE=∠CED﹣∠AED.
∴∠ADB=∠AEC.
在△ADB和△AEC中,
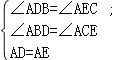
∴△ADB≌△AEC.
∴AB=AC.
(2)解:∵2∠ABC=140°,
∴∠ABC=70°.
∵AB=AC,
∴∠ABC=∠ACB=70°.
∴∠BAC=180°﹣∠ABC﹣∠ACB=40°.
∵△ADB≌△AEC,
∴∠DAB=∠EAC.
∵∠DAE=140°,
∴∠BAD=![]() (360°﹣140°﹣40°)=90°.
(360°﹣140°﹣40°)=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B坐标分别为A(1,0)、B(0,2),若将线段AB平移到A1B1,A与A1对应,A1、B1的坐标分别为A1(2,a),B1((b,3),则a+b= ___________ 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】点B(-3,0)在( )
A. x轴的正半轴上 B. x轴的负半轴上
C. y轴的正半轴上 D. y轴的负半轴上
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m,n是方程x2﹣2x﹣1=0的两根,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,则a的值等于( ).
A.﹣5 B.5 C.﹣9 D.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=
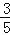 ,反比例函数y=
,反比例函数y=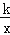 (x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .
(x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .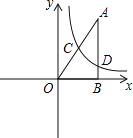
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,-1),则点B′的坐标为( )
A. (4,2) B. (5,2) C. (6,2) D. (5,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线
 (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?
相关试题

