【题目】如图,在![]() 中,弦
中,弦![]() 与弦
与弦![]() 相交于点
相交于点![]() ,
,![]() 于点
于点![]() ,过点
,过点![]() 的直线与
的直线与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() .
.
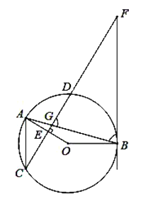
(1)若![]() ,求证:
,求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,请用
,请用![]() 表示
表示![]() 的半径;
的半径;
(3)求证:![]() .
.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据等边对等角可得∠OAB=∠OBA,然后根据OA⊥CD得到∠OAB+∠AGC=90°推出∠FBG+∠OBA=90°,从而得到OB⊥FB,再根据切线的定义证明即可;
(2)根据两直线平行,内错角相等可得∠ACF=∠F,根据垂径定理可得![]() ,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r;
,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r;
(3)连接BD,根据在同圆或等圆中,同弧所对的圆周角相等可得∠DBG=∠ACF,然后求出∠DBG=∠F,从而求出△BDG和△FBG相似,根据相似三角形对应边成比例列式表示出BG2,然后代入,整理等式左边即可得证.
(1)∵![]()
∴![]() ,
,
∵![]() ,
,
∴![]()
又∵![]() ,
,![]() ,
,
∴![]()
即![]() ,
,
∴![]()
∴![]() 是
是![]() 的切线;
的切线;
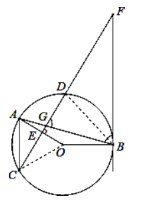
(2)∵![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即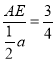 ,
,
解得![]() ,
,
连接![]() ,设圆的半径为
,设圆的半径为![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ;
;
(3)证明:连接![]() ,
,
∵![]() ,
,![]() (已证)
(已证)
∴![]()
又∵![]() ,
,
∴![]()
∴![]()
即![]() ,
,
∴![]() ,
,
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】六
 一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍. 求A、B两种品牌服装每套进价分别为多少元?
求A、B两种品牌服装每套进价分别为多少元?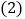 该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,将
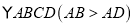 放置在第一象限,且
放置在第一象限,且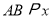 轴,直线
轴,直线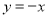 从原点出发沿
从原点出发沿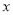 轴正方向平移,在平移过程中直线被平行四边形截得的线段长度
轴正方向平移,在平移过程中直线被平行四边形截得的线段长度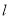 与直线在
与直线在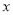 轴上平移的距离
轴上平移的距离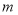 的函数图象如图2所示,则平行四边形
的函数图象如图2所示,则平行四边形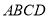 的面积为___________.
的面积为___________.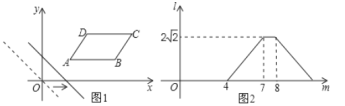
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级600名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:
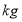 )分成五组(
)分成五组( :
: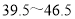 ;
;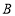 :
: ;
; :
: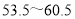 ;
;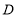 :
: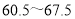 ;
; :
: ),并依据统计数据绘制了如下两幅尚不完整的统计图.
),并依据统计数据绘制了如下两幅尚不完整的统计图.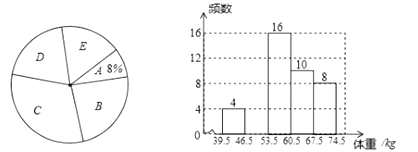
解答下列问题:
(1)这次抽样调查的样本容量是________,并补全频数分布直方图;
(2)
 组学生的频率为_________,在扇形统计图中
组学生的频率为_________,在扇形统计图中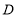 组的圆心角是__________度;
组的圆心角是__________度;(3)请你估计该校初三年级体重超过
 的学生大约有多少名?
的学生大约有多少名?
相关试题

