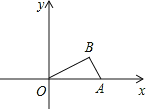
【题目】如图,直角三角形ABO放置在平面直角坐标系中,已知斜边OA在x轴正半轴上,且OA=4,AB=2,将该三角形绕着点O逆时针旋转120°后点B的对应点恰好落在一反比例函数图象上,则该反比例函数的解析式为 .
参考答案:
【答案】y=-![]() .
.
【解析】
试题分析:在Rt△ABO中,OA=4,AB=2,
∴OB=![]() ,
,
sin∠BOA=![]() ,
,
∴∠BOA=30°,
设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,
∴OB′与x轴的负半轴的夹角为30°,OB′=OB=2![]() ,
,
作B′H⊥x轴,

在Rt△OB′H中,B′H=![]() OB′=
OB′=![]() ,OH=
,OH=![]() B′H=3,
B′H=3,
∴B′点的坐标为(-3,![]() ),
),
设点B′所落在的反比例函数解析式为y=![]() ,
,
∴k=-3×![]() =-3
=-3![]()
∴该反比例函数的解析式为y=-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:

∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
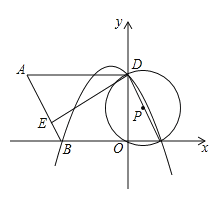
(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1),在同一方格纸中,
(1)将四边形ABCD向左平移4个单位长度,画出平移后的四边形
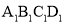 ,并写出各点的坐标;
,并写出各点的坐标;(2)将四边形ABCD绕原点O旋转180°,画出旋转后的图形四边形
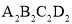 ,并写出各点的坐标.
,并写出各点的坐标.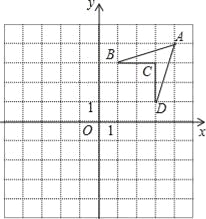
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正多边形的每个内角为150°,则这个正多边形的边数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为5cm和8cm,则等腰三角形的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣3)×|﹣2|的结果等于( )
A. 6 B. 5 C. ﹣6 D. ﹣5
相关试题

