搜索
【题目】某一广告墙PQ旁有两根直立的木杆AB和CD ， 某一时刻在太阳光下，木杆CD的影子刚好不落在广告墙PQ上，
（1）你在图中画出此时的太阳光线CE及木杆AB的影子BF；
（2）若AB=6米，CD=3米 ， CD到PQ的距离DQ的长为4米，求此时木杆AB的影长．
参考答案：
【答案】
（1）
解答：如图所示：
；
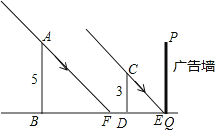（2）
设木杆AB的影长BF为x米，
由题意，得
，
解得 
．
答：木杆AB的影长是 
米．
【解析】根据木杆CD的影子刚好不落在广告墙上可以画出此时的太阳光线CE，根据太阳光线是平行的，可以画出木杆AB的影子BF；根据在同一时刻，物高与影子成比例进行求解．
【考点精析】通过灵活运用相似三角形的应用和平行投影，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解；太阳光线可以看成是平行光线，平行光线所形成的投影称为平行投影；作物体的平行投影：由于平行投影的光线是平行的，而物体的顶端与影子的顶端确定的直线就是光线，故根据另一物体的顶端可作出其影子即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，下列图案均是由完全相同的“太阳型“图标按一定的规律拼搭而成：第1个图案需要2个图标，第2个图案需要4个图标，第3个图案需要7个图标，…，按此规律，第2018个图案需要图标的个数是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】反比例函数
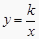在第一象限的图象如图所示，过点A（1，0）作x轴的垂线，交反比例函数 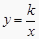的图象于点M ， △AOM的面积为3．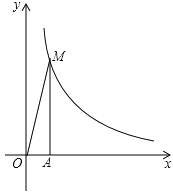
（1）求反比例函数的解析式；
（2）设点B的坐标为（t ， 0），其中t＞1．若以AB为一边的正方形有一个顶点在反比例函数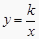 的图象上，求t的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，分别是两根木杆及其影子的图形．
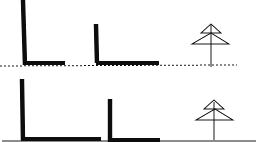
（1）哪个图形反应了阳光下的情形？哪个图反映了路灯下的情形？
（2）请你画出图中表示小树影长的线段． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了从甲乙两人中选拔一人参加初中数学竞赛，每个月对他们进行一次测试，如图绘出了两个人赛前 5 次测验成绩(每次测验成绩都是 5 的倍数).
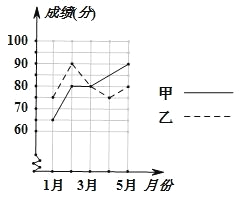
(1)分别求出甲乙两人 5 次测验成绩的平均数与方差；
(2)如果你是他们的辅导老师，应该选拔哪位学生参加这次竞赛，并简要说明理由.
-
科目： 来源： 题型：
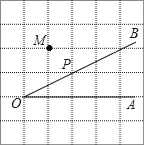
查看答案和解析>>【题目】如图，点P是∠AOB的边OB上的一点．
（1）过点M画OB的平行线MN；
（2）过点P画OA的垂线，垂足为H；
（3）过点P画OB的垂线，交OA于点C：
则线段PH的长度是点P到 的距离， 是点C到直线OB的距离，因为直线外一点到直线上各点连接的所有线段中，垂线段最短，所以线段PC、PH、OC这三条线段大小关系是 ．（用“＜”号连接）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：
（1）小明总共剪开了_______条棱．
（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．
（3）小明说：他所剪的所有棱中，最长的一条棱是最短的一条棱的5倍．现在已知这个长方体纸盒的底面是一个正方形，并且这个长方体纸盒所有棱长的和是880cm，求这个长方体纸盒的体积．
相关试题
