【题目】如图1.平面直角坐标系![]() 为原点,长方形
为原点,长方形![]() 的顶点
的顶点![]() 在坐标轴上,点
在坐标轴上,点![]() ,
,![]() ,且己知
,且己知![]() 是64的立方根,
是64的立方根,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)如图1,有两动点![]() 点从
点从![]() 点出发沿
点出发沿![]() 轴负方向以1个单位长度每秒的速度匀速移动,
轴负方向以1个单位长度每秒的速度匀速移动,![]() 点从
点从![]() 点出发以2个单位长度每秒的速度沿
点出发以2个单位长度每秒的速度沿![]() 的路线匀速移动,
的路线匀速移动,![]() 点到达
点到达![]() 点整个运动随之结束.若长方形对角线
点整个运动随之结束.若长方形对角线![]() 的交点
的交点![]() 的坐标是
的坐标是![]() ,设运动时间为
,设运动时间为![]() 秒,问:以
秒,问:以![]() 为顶点的多边形面积是否为定值,若是,请求出此多边形的面积;若不是,请说明理由.
为顶点的多边形面积是否为定值,若是,请求出此多边形的面积;若不是,请说明理由.
(3)如图2,![]() 是线段
是线段![]() 上一点,使
上一点,使![]() ,点
,点![]() 是线段
是线段![]() 上任意一点(
上任意一点(![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,求
,求![]() 的值.
的值.

参考答案:
【答案】(1)![]() ,
,![]() ;(2),以
;(2),以![]() 为顶点的多边形面积为定值,值为2;(3)
为顶点的多边形面积为定值,值为2;(3)![]()
【解析】
(1)根据![]() 是64的立方根,
是64的立方根,![]() ,求得a和b的值即可;
,求得a和b的值即可;
(2)当0<t<2时;当t=2时;当2<t<3时,当t=3时,求出多边形的面积,即可证明;
(3))设![]() ,
,![]() ,用x和y表示出∠EOC,∠OEC,∠OGC,∠OAC,代入
,用x和y表示出∠EOC,∠OEC,∠OGC,∠OAC,代入![]() 中,即可求值.
中,即可求值.
解:(1)∵![]() 是64的立方根,
是64的立方根,![]() ,
,
∴a=4,b=2,
∴![]() ,
,![]() ;
;
(2)以![]() 为顶点的多边形面积为定值.理由如下:
为顶点的多边形面积为定值.理由如下:
①当![]() 时,
时,
![]()
![]()
![]() ,
,
②当![]() 时,
时,
![]() ,
,
③当![]() 时,
时,
![]()
![]()
![]()
![]() ,
,
④当![]() 时,
时,
![]() ,
,
综上所述,以![]() 为顶点的多边形面积为定值,值为2.
为顶点的多边形面积为定值,值为2.
(3)设![]() ,
,![]() ,
,
∴![]() ,
,
在△AEC中,![]() ,
,
在△OCG中,![]() ,
,
在△AOC中,![]() ,
,
原式![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(
 ,
, m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )A. x>
 B.
B.  <x<
<x< C. x<
C. x< D. 0<x<
D. 0<x<
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.

(1)求抛物线的表达式;
(2)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(3)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,若购进2台甲型号手机和1台乙型号手机,共需要资金2800元;若购进3台甲型号手机和2台乙型号手机,共需要资金4600元.
(1)求甲、乙型号手机每台进价为多少元?
(2)该店计划购进甲、乙两种型号的手机销售,预计用不多于1.8万元且不少于1.74万元的资金购进这两种手机共20台,请问有几种进货方案?请写出进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B分别在反比例函数y=
 (x>0),y=
(x>0),y=  (x>0)的图象上且OA⊥OB,则tanB为( )
(x>0)的图象上且OA⊥OB,则tanB为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )
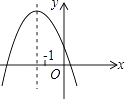
A.b2﹣4ac<0
B.abc<0
C.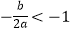
D.a﹣b+c<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是AC的中点,B是线段AC上任意一点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )

A.MN=OCB.MO=
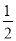 (AC-AB)
(AC-AB)C.ON=
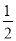 (AC - CB)D.MN=
(AC - CB)D.MN=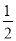 (AC+OB)
(AC+OB)
相关试题

