【题目】在矩形ABCD中,AD=8,AB=6,点E为射线DC上一个动点,把△ADE沿AE折叠,使点D落在点F处,若△CEF为直角三角形时,DE的长为 . 
参考答案:
【答案】![]() 或8
或8
【解析】解:∵四边形ABCD是矩形, ∴∠D=∠B=90°,CD=AB=6,
∴AC= ![]() =
= ![]() =10,
=10,
当△CEF为直角三角形时,有两种情况:
①当点F落在矩形内部时,F落在AC上,如图1所示.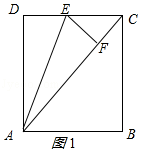
由折叠的性质得:EF=DE,AF=AD=8,
设DE=x,则EF=x,CE=6﹣x,
∴CE=6﹣x,
在Rt△CEF中,由勾股定理得:
∵EF2+CF2=CE2 ,
∴x2+22=(6﹣x)2 ,
解得x= ![]() ,
,
∴DE= ![]() ;
;
②当点F落在AB边上时,如图2所示.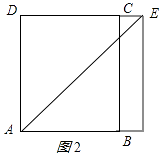
此时ADEF为正方形,
∴DE=AD=8.
③当点F落在AB边上时,易知BF= ![]() =2
=2 ![]() ,设DE=EF=x,
,设DE=EF=x,
在Rt△EFC中,x2=(6﹣x)2+(8﹣2 ![]() )2 ,
)2 ,
∴x= ![]() ,
,
∴DE= ![]() ,
,
综上所述,BE的长为 ![]() 或8或
或8或 ![]() .
.
所以答案是: ![]() 或8.
或8.
【考点精析】根据题目的已知条件,利用矩形的性质和翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=
 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( ) 
A.36
B.12
C.6
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )

A.
B.
C.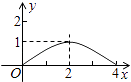
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某食品厂“端午节”期间,为了解市民对肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)四种不同口味粽子的喜爱情况,对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 请根据以上信息回答:

(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整.
(3)若居民区有6000人,请估计爱吃C粽的人数? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线;
(2)若BC=2 ,E是半圆
,E是半圆  上一动点,连接AE、AD、DE. 填空:
上一动点,连接AE、AD、DE. 填空:
①当 的长度是时,四边形ABDE是菱形;
的长度是时,四边形ABDE是菱形;
②当 的长度是时,△ADE是直角三角形.
的长度是时,△ADE是直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3800米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
相关试题

