搜索
【题目】如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= 
在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC﹣S△BAD为（ ） 
A.36
B.12
C.6
D.3
参考答案：
【答案】D
【解析】解：设△OAC和△BAD的直角边长分别为a、b， 则点B的坐标为（a+b，a﹣b）．
∵点B在反比例函数y= 
的第一象限图象上，
∴（a+b）×（a﹣b）=a2﹣b2=6．
∴S△OAC﹣S△BAD= 
a2﹣ b2= （a2﹣b2）= ×6=3．
故选D．
设△OAC和△BAD的直角边长分别为a、b，结合等腰直角三角形的性质及图象可得出点B的坐标，根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=ax2+bx+c的图象如图所示，则一次函数y=ax+b与反比例函数y=
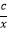在同一平面直角坐标系内的图象大致为（ ） 
A.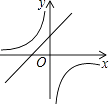
B.
C.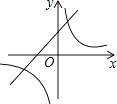
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的袋子中装有仅颜色不同的2个红球和2个白球，两个人依次从袋子中随机摸出一个小球不放回，则第一个人摸到红球且第二个人摸到白球的概率是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径画弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=
AB中，一定正确的是（ ） 
A.①②③
B.①②④
C.①③④
D.②③④ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知正方形ABCD的边长为4，E是BC边上的一个动点，AE⊥EF，EF交DC于点F，设BE=x，FC=y，则当点E从点B运动到点C时，y关于x的函数图象是（ ）
A.
B.
C.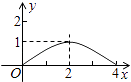
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，AD=8，AB=6，点E为射线DC上一个动点，把△ADE沿AE折叠，使点D落在点F处，若△CEF为直角三角形时，DE的长为 ．
相关试题
