Question

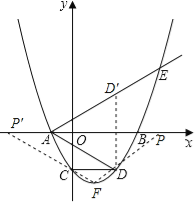
【题目】如图，二次函数y=a(x2-2mx-3m2)（其中a，m为常数，且a>0，m>0）的图象与x轴分别交于点A、B（点A位于点B左侧），与y轴交于点C(0，-3)，点D在二次函数图象上，且CD∥AB，连AD；过点A作射线AE交二次函数于点E，使AB平分∠DAE．

（1）当a=1时，求点D的坐标；

（2）证明：无论a、m取何值，点E在同一直线上运动；

（3）设该二次函数图象顶点为F，试探究：在x轴上是否存在点P，使以PF、AD、AE为边构成的三角形是以AE为斜边的直角三角形？如果存在，请用含m的代数式表示点P的横坐标，如果不存在，请说明理由．

Answer 1

【答案】（1）D(2，－3)；（2）证明见解析；（3）P(－3m，0)或(5m，0).

【解析】试题分析：（1）根据题意将a=1，C（0，﹣3）代入y=a（x2﹣2mx﹣3m2），进而求出m的值，即可得出答案；

（2）首先根据题意表示出A，B，C，D，进而联立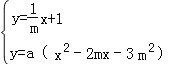，求出E点坐标即可得出答案；

（3）由（2）得：F（m，﹣4）、E（4m，5）、A（﹣m，0）、D（2m，﹣3），再利用PF，AD，AE的关系得出答案．

解：（1）当a=1时，y=a（x2﹣2mx﹣3m2）=x2﹣2mx﹣3m2，

∵与y轴交于点C（0，﹣3），

∴﹣3m2=﹣3，

解得：m=±1，

∵m＞0，

∴m=1，

∴抛物线解析式为：y=x2﹣2x﹣3=（x﹣1）2+4，

故抛物线顶点坐标为：D（2，﹣3）；

（2）作D关于AB对称的点D′必在AE上，

当y=0，则0=a（x2﹣2mx﹣3m2），

解得：x1=﹣m，x2=3m，

当x=0，y=﹣3am2，

可得：A（﹣m，0）、B（3m，0），C（0，﹣3am2），D（2m，﹣3am2）

∴D′（2m，3am2），

∵抛物线过点C，

∴﹣3am2=﹣3，

则am2=1，

∴直线AD′的解析式为：y=x+1，

联立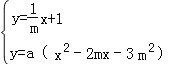，整理得x2﹣3mx﹣4m2=0

解得x1=4m，x2=﹣m（舍去）

∴E（4m，5）

∴E在y=5上运动；

（3）由（2）得：F（m，﹣4）、E（4m，5）、A（﹣m，0）、D（2m，﹣3）

设P（b，0）

∴PF2=（m﹣b）2+16，AD2=9m2+9，AE2=25m2+25

∴（m﹣b）2+16+9m2+9=25m2+25，

解得：b1=﹣3m，b2=5m

∴P（﹣3m，0）或（5m，0）．