【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( ) 
A.1:3
B.1:5
C.1:6
D.1:11
参考答案:
【答案】C
【解析】解:∵O为平行四边形ABCD对角线的交点, ∴DO=BO,
又∵E为OD的中点,
∴DE= ![]() DB,
DB,
∴DE:EB=1:3,
又∵AB∥DC,
∴△DFE∽△BAE,
∴ ![]() =(
=( ![]() )2=
)2= ![]() ,
,
∴S△DEF= ![]() S△BAE ,
S△BAE ,
∵ ![]() =
= ![]() ,
,
∴S△AOB= ![]() S△BAE ,
S△BAE ,
∴S△DEF:S△AOB= ![]() =1:6,
=1:6,
故选C.
根据平行四边形的性质可知BO=DO,又因为E为OD的中点,所以DE:BE=1:3,根据相似三角形的性质可求出S△DEF:S△BAE . 然后根据 ![]() =
= ![]() ,即可得到结论.
,即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·
 )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B,抛物线y=﹣
 (x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
(x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.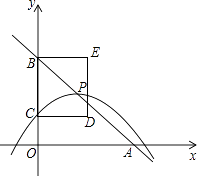
(1)n=(用含m的代数式表示),点C的纵坐标是(用含m的代数式表示);
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数解析式;
(3)直接写出矩形BCDE有两个顶点落在抛物线上时m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小红同学四次中考数学模拟考试成绩分别是:96,104,104,116,关于这组数据下列说法错误的是( )
A.平均数是105
B.众数是104
C.中位数是104
D.方差是50 -
科目: 来源: 题型:
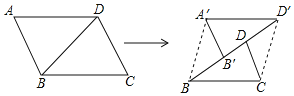
查看答案和解析>>【题目】如图,平行四边形硬纸片ABCD中,
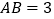 ,
,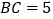 ,
, ,沿着对角线BD将平行四边形剪开成两个三角形,固定
,沿着对角线BD将平行四边形剪开成两个三角形,固定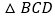 不动,将
不动,将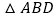 沿射线BD方向以每秒1个单位的速度匀速运动
沿射线BD方向以每秒1个单位的速度匀速运动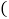 运动后
运动后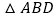 记为
记为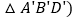 连接
连接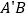 和
和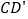 .
.
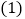 小明认为在运动过程中,始终有
小明认为在运动过程中,始终有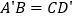 ,你同意吗?请说明理由.
,你同意吗?请说明理由.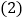 保持上述条件不变,当
保持上述条件不变,当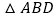 运动______秒时,四边形
运动______秒时,四边形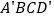 为菱形.
为菱形.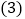 保持上述条件不变,当
保持上述条件不变,当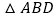 运动______秒时,四边形
运动______秒时,四边形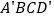 为矩形.
为矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正比例函数
 与反比例函数
与反比例函数 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为 其中
其中 .
. 四边形ABCD的是______
四边形ABCD的是______ 填写四边形ABCD的形状
填写四边形ABCD的形状
 当点A的坐标为
当点A的坐标为 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值. 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在
 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 .
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 . 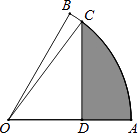
相关试题

