【题目】如图,平面直角坐标系中,A(﹣3,﹣2)、B(﹣1,﹣4)
(1)直接写出:S△OAB= ;
(2)延长AB交y轴于P点,求P点坐标;
(3)Q点在y轴上,以A、B、O、Q为顶点的四边形面积为6,求Q点坐标.

参考答案:
【答案】(1)5;(2)(0,﹣5);(3) (0, ![]() )或(0,﹣2).
)或(0,﹣2).
【解析】试题解析:(1)延长AB交y轴于P点,如图,利用待定系数法求出直线AB的解析式为y=-x-5,则得到P(0,-5),然后根据三角形面积公式和利用S△OAB=S△AOP-S△OBP进行计算即可;
(2)由(1)得到P点的坐标;
(3)分类讨论:当Q在y轴的正半轴上时,利用S四边形ABOQ=S△AOB+S△AOQ得到S△AOQ=1,再根据三角形面积公式求出OQ.从而得到Q点坐标;当Q在y轴的负半轴上时,利用S四边形ABOQ=S△AOB+S△BOQ得到S△BOQ=1,再根据三角形面积公式求出OQ.从而得到Q点坐标.
试题解析:(1)延长AB交y轴于P点,如图,
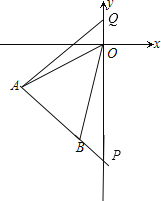
设直线AB的解析式为y=kx+b,
把A(﹣3,﹣2)、B(﹣1,﹣4)代入得![]()
解得![]() .
.
所以直线AB的解析式为y=﹣x﹣5,
当x=0时,y=﹣x﹣5=﹣5,则P(0,﹣5),
所以S△OAB=S△AOP﹣S△OBP
=![]() ×5×3﹣
×5×3﹣![]() ×5×1
×5×1
=5.
(2)由(1)得到P点的坐标为(0,﹣5);
(3)当Q在y轴的正半轴上时,∵S四边形ABOQ=S△AOB+S△AOQ,
∴S△AOQ=6﹣5=1,
∴![]() ×3×OQ=1,
×3×OQ=1,
解得OQ=![]() .
.
则此时Q点的坐标为(0, ![]() );
);
当Q在y轴的负半轴上时,
∵S四边形ABOQ=S△AOB+S△BOQ,
∴S△BOQ=1,
∴S△AOQ=6﹣5=1,
∴![]() ×1×OQ=1,
×1×OQ=1,
解得OQ=2,
则此时Q点的坐标为(0,﹣2),
即Q点坐标为(0, ![]() )或(0,﹣2).
)或(0,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )

A.
 B.
B. C.
C. D.
D.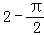
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.

(1)求证:四边形EGFH是菱形;
(2)若AB=1,则当∠ABC+∠DCB=90°时,求四边形EGFH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,C(0,5)、D(a,5)(a>0),A、B在x轴上,∠1=∠D,请写出∠ACB和∠BED数量关系以及证明.
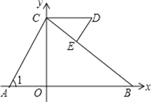
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+2b+4的图象经过点(-1,-3),k满足|k-3|=4,且y随x的增大而减小,求此一次函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点p(5.﹣3)关于原点对称的点的坐标是( )
A.(3,﹣5)
B.(﹣5,﹣3)
C.(﹣5,3)
D.(﹣3,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】若10m=5,10n=3,则102m+3n=
相关试题

