【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.

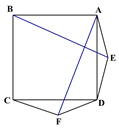

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
参考答案:
【答案】(1)AF=BE,AF⊥BE(2)结论成立(3)结论都能成立
【解析】试题分析:(1)根据正方形和等边三角形可证明△ABE≌△DAF,然后可得BE=AF,∠ABE=∠DAF,进而通过直角可证得BE⊥AF;
(2)类似(1)的证法,证明△ABE≌△DAF,然后可得AF=BE,AF⊥BE,因此结论还成立;
(3)类似(1)(2)证法,先证△AED≌△DFC,然后再证△ABE≌△DAF,因此可得证结论.
试题解析:解:(1)AF=BE,AF⊥BE.
(2)结论成立.
证明:∵四边形ABCD是正方形,
∴BA="AD" =DC,∠BAD =∠ADC = 90°.
在△EAD和△FDC中,
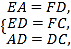
∴△EAD≌△FDC.
∴∠EAD=∠FDC.
∴∠EAD+∠DAB=∠FDC+∠CDA,
即∠BAE=∠ADF.
在△BAE和△ADF中,
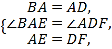
∴△BAE≌△ADF.
∴BE = AF,∠ABE=∠DAF.
∵∠DAF +∠BAF=90°,
∴∠ABE +∠BAF=90°,
∴AF⊥BE.
(3)结论都能成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 于
于 ,且
,且 .
.(
 )求证:
)求证: .
.(
 )若
)若 ,
, 于
于 ,
, 为
为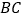 中点,
中点, 与
与 ,
, 分别交于点
分别交于点 ,
, .
.①判断线段
 与
与 相等吗?请说明理由.
相等吗?请说明理由.②求证:
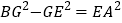 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种运算(a*b)=2a×(a+b),则4*5=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+y2+2x﹣6y+10=0,求x+y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:无论x、y为何值,4x2-12x+9y2+30y+35的值恒为正.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
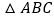 中,
中, ,
, ,
,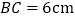 ,若动点
,若动点 从点
从点 开始,按
开始,按 的路径
的路径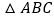 运动一周,且速度为每秒
运动一周,且速度为每秒 ,设运动的时间为
,设运动的时间为 秒.
秒.(
 )求
)求 为何值时,
为何值时, 把
把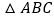 的周长分成相等的两部分
的周长分成相等的两部分(
 )求
)求 为何值时,
为何值时, 把
把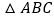 的面积分成相等的两部分;并求此时
的面积分成相等的两部分;并求此时 的长.
的长.(
 )求
)求 为何值时,
为何值时, 为等腰三角形?(请直接写出答案)
为等腰三角形?(请直接写出答案)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车从甲地匀速行使至乙地,一辆快车同时从乙地匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(h)的对应关系如图所示,当两车相距300km时,x为________h.

相关试题

