【题目】如图,△ABC的角平分线相交于P,∠A=m°,
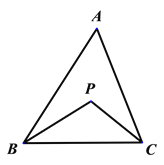
(1)若∠A=40°,求∠BPC的度数;
(2)设△ABC的外角∠CBD、∠BCE的平分线相交于Q, 且∠A=m°,求∠BQC的度数

(3)设△ABC的外角∠CBD、∠BCE的n等分线相交于R,且∠A=m°,∠CBR=![]() ∠CBD,∠BCR=
∠CBD,∠BCR=![]() ∠BCE,求∠BRC的度数
∠BCE,求∠BRC的度数
参考答案:
【答案】(1)110°
(2)90°+![]() m°
m°
(3)![]() ×180°-
×180°-![]() (此结果形式可以不同,只要正确皆可)
(此结果形式可以不同,只要正确皆可)
【解析】试题分析:(1)根据三角形内角和定理和角平分线的性质解答即可;
(2)(3)根据三角形内角和定理和三角形外角的性质解答即可.
试题解析:解:(1)∵∠A=40°,∴∠ABC+∠ACB=180°-40°=140°.∵BP、CP是角平分线,∴∠ABC=2∠PBC,∠ACB=2∠PCB,∴∠PBC+∠PCB=![]() (∠ABC+∠ACB)==
(∠ABC+∠ACB)==![]() ×140°=70°,∴∠P=180°-70°=110°.
×140°=70°,∴∠P=180°-70°=110°.
(2)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,∴∠DBC+∠BCD=2∠A+∠ABC+∠ACB=∠A+180°=m+180°.∵BQ,CQ是角平分线,∴∠DBC=2∠QBC,∠BCE=2∠BCQ,∴∠QBC+∠BCQ=![]() (∠DBC+∠ECB)=
(∠DBC+∠ECB)=![]() (m+180°)=90°+
(m+180°)=90°+![]() m.在△BCQ中,∠Q=180°-(∠QBC+∠BCQ)=180°-(90°+
m.在△BCQ中,∠Q=180°-(∠QBC+∠BCQ)=180°-(90°+![]() m)=90°-
m)=90°-![]() m.
m.
(3)由(2)得:∠DBC+∠BCD=m+180°,∠RBC+∠BCR=![]() (∠DBC+∠ECB)=
(∠DBC+∠ECB)=![]() (m+180°).在△BCR中,∠R=180°-(∠RBC+∠BCR)=180°-
(m+180°).在△BCR中,∠R=180°-(∠RBC+∠BCR)=180°-![]() (m+180°)=
(m+180°)=![]() .
.
-
科目: 来源: 题型:
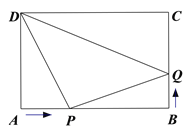
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
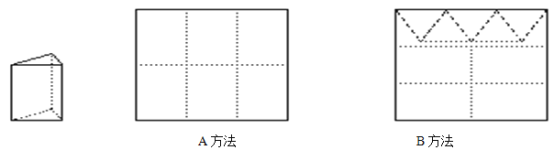
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区内有一块长、宽比为2∶1的矩形空地,计划在该空地上修筑两条宽均为2 m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312 m2,请求出原来大矩形空地的长和宽.
(1)请找出上述问题中的等量关系:_________________;
(2)若设大矩形空地的宽为xm,可列出的方程为_____________,方程的解为__________,原来大矩形空地的长和宽分别为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,它的三边长是三个连续的正偶数,且AC>BC.
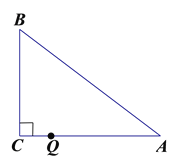
(1)这个直角三角形的各边长;
(2)若动点Q从点C出发,沿CA方向以1个单位长度/秒的速度运动,到达点A停止运动,请运用尺规作图作出以点Q为圆心,QC为半径,且与AB边相切的圆,并求出此时点Q的运动时间.
(3) 若动点Q从点C出发,沿CA方向以1个单位长度/秒的速度运动,到达点A停止运动,以Q为圆心、QC长为半径作圆,请探究点Q在整个运动过程中,运动时间t为怎样的值时,⊙Q与边AB分别有0个公共点、1个公共点和2个公共点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:

两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数
 、
、 、
、 ,有
,有 ,所以
,所以 为
为 和
和 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到 和
和 的中间分数
的中间分数 ,
,  ,
,  ,
,  .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到 和
和 更多的中间分数.
更多的中间分数.(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的
 和
和 的中间分数是 ;
的中间分数是 ;(2)写出分数
 和
和 (a、b、c、d均为正整数,
(a、b、c、d均为正整数,  ,
,  )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;(3)若
 与
与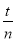 (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是 和
和 的中间分数,则
的中间分数,则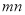 的最小值为 .
的最小值为 .
相关试题

