【题目】如图所示,在△ABC中,AD是BC边上的中线.
(1)画出与△ACD关于点D成中心对称的三角形;

(2)找出与AC相等的线段;
(3)探究:△ABC中AB与AC的和与中线AD之间有何大小关系?并说明理由;
(4)若AB=5,AC=3,求线段AD的取值范围.
参考答案:
【答案】(1)△A′BD即为所求(2)A′B=AC(3)AB+AC>2AD(4)1<AD<4.
【解析】【试题分析】
(1)根据成中心对称的定义,延长AD到A’,使A’D=AD,点C与点B关于点D对称,连接A’B即可,△A′BD即为所求;
(2)根据成中心对称的两个图形 对应边相等,得A′B=AC;
(3)由(2)得:AB+AC=AB+A′B,根据三角形两边之和大于第三边,得AB+A′B >AA’=2AD,即AB+AC>2AD;
(4)由(3)得,根据三角形两边之和大于第三边,两边之差小于第三边,得5-3<AA’=2AD<5+3,即2<2AD<8,所以1<AD<4.
【试题解析】
(1)如图所示,△A′BD即为所求;

(2)A′B=AC;
(3)AB+AC>2AD,理由:由于△A′BD与△ACD关于点D成中心对称,所以AD=A′D,AC=A′B,在△ABA′中,有AB+A′B>AA′,即AB+AC>AD+A′D,因此AB+AC>2AD;
(4)由(3)可得,在△ABA′中,有AB-A′B<AA′<AB+A′B,即AB-AC<2AD<AB+AC,因此有2<2AD<8,所以1<AD<4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.

(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°,得到△FEC
(1)猜想AE与BF有何关系,说明理由.
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
(3)当∠ACB为多少度时,四边形ABFE为矩形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点△A′B′C′是由格点△ABC通过怎样的变换得到的?
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.
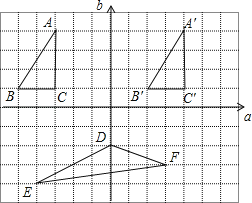
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△DEF是由△ABC绕点O顺时针旋转180°后形成的图形;
(1)请你指出图中所有相等的线段;
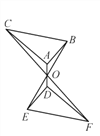
(2)图中哪些三角形可以被看成是关于点O成中心对称关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
相关试题

