【题目】如图,已知点A(1,a)与点B(b,1)在反比例函数y=![]() (x>0)图象上,点P(m,0)是x轴上的任意一点,若△PAB的面积为2,此时m的值是______.
(x>0)图象上,点P(m,0)是x轴上的任意一点,若△PAB的面积为2,此时m的值是______.

参考答案:
【答案】﹣1或7
【解析】
把点A(1,a)与点B(b,1)代入反比例函数y=![]() (x>0),求出A,B坐标,延长AB交x轴于点C,如图2,设直线AB的解析式为y=mx+n,求出点C的坐标,用割补法求出PC的值,结合点C的坐标即可.
(x>0),求出A,B坐标,延长AB交x轴于点C,如图2,设直线AB的解析式为y=mx+n,求出点C的坐标,用割补法求出PC的值,结合点C的坐标即可.
解:∵点A(1,a)与点B(b,1)在反比例函数y=![]() (x>0)图象上,
(x>0)图象上,
∴a=2,b=2,
∴点A(1,2)与点B(2,1),
延长AB交x轴于点C,如图2,
设直线AB的解析式为y=mx+n,
则有![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=﹣x+3.
∵点C是直线y=﹣x+3与x轴的交点,
∴点C的坐标为(3,0),OC=3,
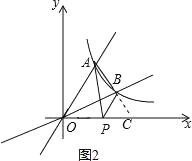
∵S△PAB=2,
∴S△PAB=S△PAC﹣S△PBC=![]() ×PC×2﹣
×PC×2﹣![]() ×PC×1=
×PC×1=![]() PC=2,
PC=2,
∴PC=4.
∵C(3,0),P(m,0),
∴|m﹣3|=4,
∴m=﹣1或7,
故答案为:﹣1或7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四点A、B、C、D;
(1)画射线AD;(不需写作图过程)
(2)求作点P,使PA+PB+PC+PD的值最小;(不需写作图过程)
(3)在(2)的条件下,若S△ABP=2,S△ADP=6,S△BCP=1.5,则S△DCP= .
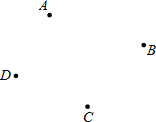
-
科目: 来源: 题型:
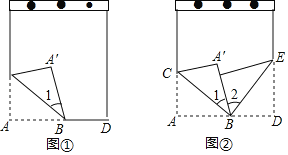
查看答案和解析>>【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在A′处,BC为折痕;
(1)图①中,若∠1=30°,则∠A′BD=_____;
(2)如果在图②中改变∠1的大小,则BA的位置也随之改变,又将活页的另一角斜折过去,使BD边与BA′重合,折痕为BE.那么∠CBE的度数是否会发生变化呢?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1.
(2)以原点O为位似中心,在原点的另一个侧画出△A2B2C2.使
 =
= ,并写出A2、B2、C2的坐标.
,并写出A2、B2、C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y1=mx的图象与反比例函数y2=
 (m为常数,m≠0)的图象有一个交点的横坐标是2.
(m为常数,m≠0)的图象有一个交点的横坐标是2.(1)求m的值;
(2)写出当y1<y2时,自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题:
操作次数
1
2
3
4
…
正方形个数
4
7
…
(1)如果剪100次,共能得到 个正方形;
(2)如果剪n次共能得到bn个正方形,试用含有n、bn的等式表示它们之间的数量关系 ;
(3)若原正方形的边长为1,设an表示第n次所剪的正方形的边长,试用含n的式子表示an ;
(4)试猜想a1+a2+a3+a4+…+an﹣1+an与原正方形边长的数量关系,并用等式写出这个关系 .

-
科目: 来源: 题型:
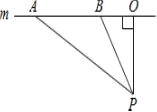
查看答案和解析>>【题目】随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
(1)求A、B之间的路程(保留根号);
(2)已知本路段对校车限速为12米/秒若测得某校车从A到B用了2秒,这辆校车是否超速?请说明理由.
相关试题

