【题目】在一个不透明的袋子中装着5个完全相同的小球,分别标有数字0,1,,2,-1,-2,从袋中随机取出一个小球。
(1)随机地从布袋中摸出一个小球,则摸出的球上数字为正数的概率为
(2)若第一次从布袋中随机摸出一个小球,设记下的数字为x,再将此球放回盒中,第二次再从布袋中随机抽取一张,设记下的数字为y,记M(x,y),请用画树状图或列表法列举出点M所有可能的坐标,并求点M位于第二象限的概率.
参考答案:
【答案】
(1)![]()
(2)解:画树状图得:
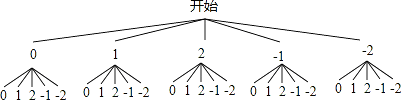
∵共有25种等可能的结果,点M恰好落在第二像限的有4种情况,
∴点M恰好落在第二像限的概率为: ![]() .
.
【解析】(1)根据装着5个完全相同的小球,正数有2个,得到摸出的球上数字为正数的概率;(2)根据画树状图得出共有25种等可能的结果,点M恰好落在第二像限的有4种情况,求出点M恰好落在第二像限的概率.
【考点精析】本题主要考查了随机事件和列表法与树状图法的相关知识点,需要掌握在条件S下,一定会发生的事件,叫相对于条件S的必然事件;在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;在条件S下可能发生也可能不发生的事件,叫相对于S的随机事件;当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD.∠1=∠2,∠3=∠4,试说明 AD∥BE,请你将下面解答过程填写完整.

解:∵AB∥CD,
∴∠4= ( )
∵∠3=∠4
∴∠3= (等量代换)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAE 即∠BAE= .
∴∠3= ( )
∴AD∥BE( ).
-
科目: 来源: 题型:
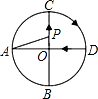
查看答案和解析>>【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
A.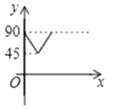
B.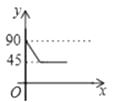
C.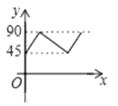
D.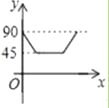
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别
平均分
中位数
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%

(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明上午8点正从家里出发,到书店买书.右图反映了小明买书过程中(从出发到回家)离家的距离y(米)和离家的时间x(分)的关系.

(1)书店离小明家多远?
(2)若小明离开书店返回家时的平均速度比去书店时的平均速度每分钟快15米,问小明几点到家并求小明离开书店后返家过程中y与x的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】大楼AD的高为10米,不远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D点测得塔顶B点的仰角为30°,求塔BC的高度.
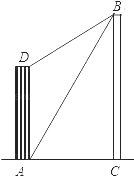
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.

(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r .
相关试题

