【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1,当点A1落在AC上时.
(1)如图,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
(2)如图,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)证△ABA1是等边三角形,得∠AA1B=∠A1BD1,由AC∥BD1,AC=BD1,可得;(2)连接BD1.证△BCD1≌D1A1B,得四边形ABD1C是平行四边形,再证△OCD1≌△OBA(AAS),△DCO≌△ABO(SAS),可得DO=OA.
证明:(1)如图1中,
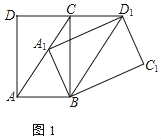
∵∠BAC=60°,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=60°,
∴∠AA1B=∠A1BD1,
∴AC∥BD1,
∵AC=BD1,
∴四边形ABD1C是平行四边形.
(2)如图2中,连接BD1.
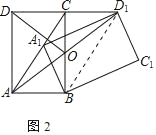
∵∠BCD1=∠BAD1=90°,BD1=D1B,BC=A1D1,
∴△BCD1≌D1A1B,
∴CD1=BA1,
∵BA=BA1,
∴AB=CD1,∵AC=BD1
∴四边形ABD1C是平行四边形,
∴CD1∥AB,CD1=AB,
∠OCD1=∠ABO,
∵∠COD1=∠AOB,
∴△OCD1≌△OBA(AAS),
∴OC=OB,
∵CD=BA,∠DCO=∠ABO,
∴△DCO≌△ABO(SAS),
∴DO=OA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
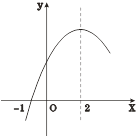
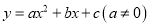 的部分图象如图③所示,图象过点(-1,0),对称轴为直线
的部分图象如图③所示,图象过点(-1,0),对称轴为直线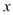 =2,则下列结论中正确的个数有( )
=2,则下列结论中正确的个数有( )①4
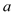 +b=0;②
+b=0;②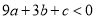 ;③若点A(-3,
;③若点A(-3, 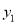 ),点B(-
),点B(-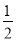 ,
, 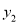 ),点C(5,
),点C(5, 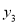 )在该函数图象上,则
)在该函数图象上,则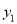 <
<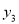 <
<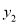 ;④若方程
;④若方程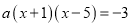 的两根为
的两根为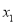 和
和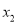 ,且
,且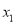 <
<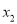 ,则
,则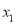 <-1<5<
<-1<5<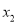 .
. 
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数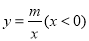 的图象交于A(-1,3),B(-3,n)两点,直线
的图象交于A(-1,3),B(-3,n)两点,直线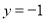 与
与 轴交于点C.
轴交于点C.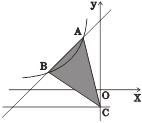
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
-
科目: 来源: 题型:
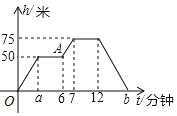
查看答案和解析>>【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S.
(1)求S关于x的函数解析式;
(2)当EFGH是正方形时,求S的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几
获奖作品的件数
一等奖

b
二等奖
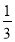
c
三等奖
a
96
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的
 ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的 ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的 ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.

(1)求证:PA是⊙O的切线;
(2)若PD=
 ,求⊙O的直径.
,求⊙O的直径.
相关试题

