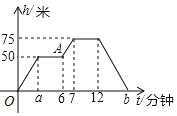
【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.
参考答案:
【答案】(1)时间(或t);高度(或h);(2)5;(3)25;(4)2;15;(5)在第6分钟时,无人机的飞行高度为50米.
【解析】
![]() 根据图象信息得出自变量和因变量即可;
根据图象信息得出自变量和因变量即可;![]() 根据图象信息得出无人机在75米高的上空停留的时间
根据图象信息得出无人机在75米高的上空停留的时间![]() 分钟即可;
分钟即可;![]() 根据速度
根据速度![]() 路程除以时间计算即可;
路程除以时间计算即可;![]() 根据速度的汽车时间即可;
根据速度的汽车时间即可;![]() 根据点的实际意义解答即可.
根据点的实际意义解答即可.
解:(1)横轴是时间,纵轴是高度,所以自变量是时间(或t),因变量是高度(或h);
(2)无人机在75米高的上空停留的时间是12-7=5分钟;
(3)在上升或下降过程中,无人机的速度![]() 米/分;
米/分;
(4)图中a表示的数是![]() 分钟;b表示的数是
分钟;b表示的数是![]() 分钟;
分钟;
(5)图中点A表示在第6分钟时,无人机的飞行高度为50米;
故答案为:时间(或t);高度(或h);5;25;2;15;在第6分钟时,无人机的飞行高度为50米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人承包了一池塘养鱼,他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼,把每条鱼都作上标记,放回鱼塘;过了2天,他让他父亲从鱼塘内打捞上了50条鱼,结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤,平均每条鱼估计2.3斤,你能帮助他估计一下今年的收入情况吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 分别是三角形
分别是三角形 的边
的边 的中点,
的中点, 是
是 所在平面上的动点,连接
所在平面上的动点,连接 ,点
,点 分别是
分别是 的中点,顺次连接点
的中点,顺次连接点

(1)如图,当点
 在
在 的内部时,求证:四边形
的内部时,求证:四边形 是平行四边形;
是平行四边形;(2)若四边形
 是菱形,则
是菱形,则 与
与 应满足怎样的关系?若四边形
应满足怎样的关系?若四边形 是矩形,则
是矩形,则 与
与 应满足怎样的关系?(直接写出答案,不需要说明理由)
应满足怎样的关系?(直接写出答案,不需要说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩“石头、剪刀、布”的游戏,他们在不透明的袋子中放入形状,大小均相同的15张卡片,其中写有“石头”、“剪刀”、“布”的卡片数分别为3、5、7张,两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出“石头”,则乙获胜的概率是多少?
-
科目: 来源: 题型:
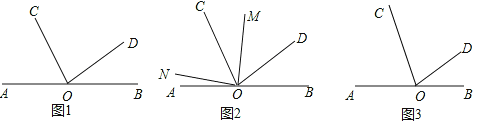
查看答案和解析>>【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=
 ∠AOC.
∠AOC.(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点B、C为线段AD上的两点,AB=
 BC=
BC= CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
相关试题

