【题目】已知关于x的方程x2﹣(2k+3)x+k2+2k=0,有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若方程的两实数根x1,x2满足x1x2﹣x12﹣x22=﹣16,求实数k的值.
参考答案:
【答案】(1)k>﹣![]() ;(2)k=1.
;(2)k=1.
【解析】试题分析:(1)根据判别式的意义得到△=(2k+3)2﹣4(k2+2k)>0,然后解不等式即可得到k的范围;
(2)根据根与系数的关系得到x1+x2=2k+3,x1x2=k2+2k,再利用完全平方公式把x1x2﹣x12﹣x22=﹣16变形为(x1+x2)2﹣3x1x2﹣16=0,则(2k+3)2﹣3(k2+2k)﹣16=0,然后解方程求出满足条件的k的值.
试题解析:解:(1)根据题意得:△=(2k+3)2﹣4(k2+2k)>0,解得:k>﹣![]() ;
;
(2)根据题意得:x1+x2=2k+3,x1x2=k2+2k,因为x1x2﹣x12﹣x22=﹣16,所以x1x2﹣[(x1+x2)2﹣2x1x2]=﹣16,即[(x1+x2)2﹣3x1x2﹣16=0,所以(2k+3)2﹣3(k2+2k)﹣16=0,解得:k1=﹣7,k2=1,而k>﹣![]() ,所以k=1.
,所以k=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的2017年12月份的月历表中,任意框出表中竖列上四个相邻的数,这四个数的和可能是:

A.60B.70C.80D.90
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当方法解下列方程组
(1)
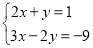 (2)
(2)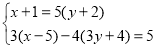
(3)
 (4)
(4)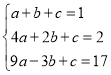
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了美化环境,计划在一定的时间内完成绿化面积
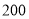 万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加
万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加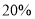 ,而且要提前
,而且要提前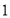 年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多
年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多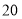 万亩,求原计划平均每年的绿化面积.
万亩,求原计划平均每年的绿化面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D,E分别为边BC,AC上一点,将△ADE沿着直线AD翻折,点E落在点F处,如果DF⊥BC,△AEF是等边三角形,那么AE=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市试销一种成本价为80元/瓶的白酒,规定试销期间单价不低于100元/瓶且不高于160元/瓶.经试销发现,销售量y(瓶)与销售单价x(元/瓶)符合一次函数关系,且x=120时,y=100;x=130时,y=95.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)当销售单价x定为每瓶多少元时,销售利润(w)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
相关试题

