【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

参考答案:
【答案】(1)x=18;(2) 416 m2.
【解析】
(1)根据“![]()
![]() ÷2”可得函数解析式;
÷2”可得函数解析式;
(2)根据矩形的面积公式列方程求解可得;
(3)根据矩形的面积公式列出总面积关于x的函数解析式,配方成顶点式后利用二次函数的性质求解可得.
(1)根据题意知,y=![]() =-
=-![]() x+
x+![]() ;
;
(2)根据题意,得(-![]() x+
x+![]() )x=384,
)x=384,
解得x=18或x=32.
∵墙的长度为24 m,∴x=18.
(3)设菜园的面积是S,则S=(-![]() x+
x+![]() )x=-
)x=-![]() x2+
x2+![]() x=-
x=-![]() (x-25)2+
(x-25)2+![]() .
.
∵-![]() <0,∴当x<25时,S随x的增大而增大.
<0,∴当x<25时,S随x的增大而增大.
∵x≤24,
∴当x=24时,S取得最大值,最大值为416.
答:菜园的最大面积为416 m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,P是抛物线y=-x2+3x上一点,且在x轴上方,过点P分别向x轴、y轴作垂线,得到矩形PMON.若矩形PMON的周长随点P的横坐标m增大而增大,则m的取值范围是_________.

-
科目: 来源: 题型:
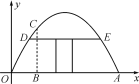
查看答案和解析>>【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为
 米.
米.(1)求该抛物线的函数关系式;
(2)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?
-
科目: 来源: 题型:
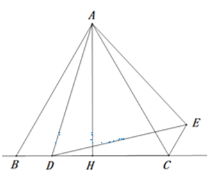
查看答案和解析>>【题目】如图,在
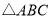 中,
中,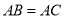 ,
, 垂足为
垂足为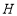 ,
,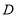 为直线
为直线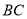 上一动点(不与点
上一动点(不与点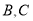 重合),在
重合),在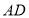 的右侧作
的右侧作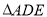 ,使得
,使得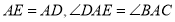 ,连接
,连接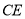 .
.(1)求证:
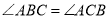 ;
;(2)当
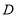 在线段
在线段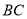 上时
上时① 求证:
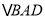 ≌
≌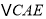 ;
; ② 若
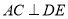 , 则
, 则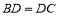 ;
;(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为(
 ,-
,- )的抛物线y=ax2+bx+c过点M(2,0).
)的抛物线y=ax2+bx+c过点M(2,0).(1)求抛线的表达式;
(2)点A是抛物线与x轴的交点(不与点M重合),点B是抛物线与y轴的交点,点C是直线y=x+1上一点(处于x轴下方),点D是反比例函数y=
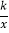 (k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.
(k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 分别在射线
分别在射线 上移动,
上移动, 的平分线与
的平分线与 的外角平分线交于点
的外角平分线交于点 .
.
(1)当
 时,
时,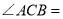 .
.(2)请你猜想:随着
 两点的移动,
两点的移动, 的度数大小是否变化?请说明理由.
的度数大小是否变化?请说明理由.
相关试题

