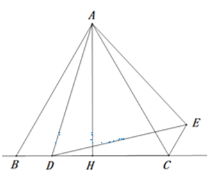
【题目】如图,在![]() 中,
中,![]() ,
,![]() 垂足为
垂足为![]() ,
,![]() 为直线
为直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),在
重合),在![]() 的右侧作
的右侧作![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 在线段
在线段![]() 上时
上时
① 求证:![]() ≌
≌![]() ;
;
② 若![]() , 则
, 则![]() ;
;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果)
参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②证明见解析;(3)20°或40°或100°.
【解析】
(1)证明Rt△AHB≌Rt△AHC(HL),即可解决问题.
(2)①根据SAS即可证明;
②D运动到BC中点(H点)时,AC⊥DE;利用等腰三角形的三线合一即可证明;
(3)分三种情形分别求解即可解决问题;
(1)∵AB=AC,AH⊥BC,
∴∠AHB=∠AHC=90°,
在Rt△AHB和Rt△ACH中,
![]() ,
,
∴Rt△AHB≌Rt△AHC(HL),
∴∠ABC=∠ACB.
(2)①如图1中,
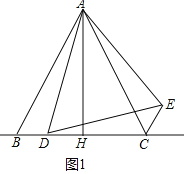
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
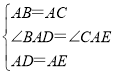 ,
,
∴△BAD≌△CAE.
②D运动到BC中点(H点)时,AC⊥DE;
理由:如图2中,∵AB=AC,AH⊥BC,
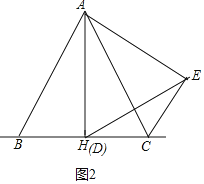
∴∠BAH=∠CAH,
∵∠BAH=∠CAE,
∴∠CAH=∠CAE,
∵AH=AE,
∴AC⊥DE.
(3)∠ADB的度数为20°或40°或100°.
理由:①如图3中,当点D在CB的延长线上时,
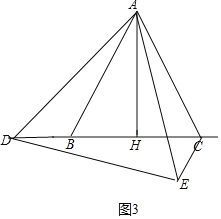
∵CE∥AB,
∴∠BAE=∠AEC,∠BCE=∠ABC,
∵△DAB≌△EAC,
∴∠ADB=∠AEC,∠ABD=∠ACE,
∴∠BAC=∠BAE+EAC=∠AEC+∠EAC=180°-∠ACE=180°-∠ABD=∠ABC=∠ACB,
∴△ABC是等边三角形,
∵△ABD中的最小角是∠BAD=20°,则∠ADB=∠ABC-∠BAD=40°.
②当点D在线段BC上时,最小角只能是∠DAB=20°,此时∠ADB=180°-20°-60°=100°.
③当点D在BC 延长线上时,最小角只能是∠ADB=20°,
综上所述,满足条件的∠ABD的值为20°或40°或100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中,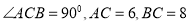 .点
.点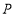 从点
从点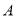 出发沿
出发沿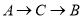 路径向终点
路径向终点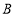 运动;点
运动;点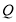 从
从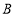 点出发沿
点出发沿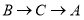 路径向终点
路径向终点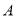 运动.点
运动.点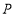 和
和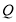 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过
分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过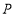 和
和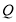 作
作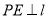 于
于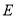 ,
,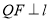 于
于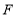 .则点
.则点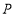 运动时间等于____________时,
运动时间等于____________时,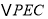 与
与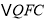 全等。
全等。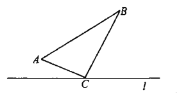
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD
(3)画出BC边上的高线AE
(4)点
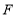 为方格纸上的格点(异于点
为方格纸上的格点(异于点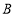 ),若
),若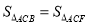 ,则图中的格点
,则图中的格点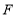 共有 个.
共有 个.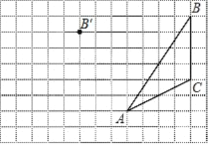
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.
(1) 求每辆小客车和每辆大客车的乘客座位数;
(2) 由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,分别探索下列四个图形中∠P、∠A、∠C,发现有如下三种数量关系:∠A+∠C =∠P ;∠P+∠A =∠C ;∠P+∠C =∠A,请你选择其中的两种数量关系说明理由.
(1)我选择的是图 ,数量关系式是 .
理由:
(2) 我选择的是图 ,数量关系式是 .
理由:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
 为坐标原点.已知:抛物线
为坐标原点.已知:抛物线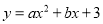 经过点
经过点 和点
和点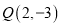 .
.(
 )试判断该抛物线与
)试判断该抛物线与 轴交点的情况.
轴交点的情况.(
 )平移这条抛物线,使平移后的抛物线经过点
)平移这条抛物线,使平移后的抛物线经过点 ,且与
,且与 轴交于点
轴交于点 ,同时满足以
,同时满足以 ,
,  ,
,  为顶点的三角形是等腰直角三角形.请你写出平移过程,并说明理由.
为顶点的三角形是等腰直角三角形.请你写出平移过程,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤
 PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.
A. 2B. 3C. 4D. 5
相关试题

