【题目】如图,在平面直角坐标系中,P是抛物线y=-x2+3x上一点,且在x轴上方,过点P分别向x轴、y轴作垂线,得到矩形PMON.若矩形PMON的周长随点P的横坐标m增大而增大,则m的取值范围是_________.

参考答案:
【答案】0<m≤2
【解析】
代入y=0求出抛物线与x轴交点的坐标,进而可得出0<m<3,由点P的横坐标可得出OM=m、PM=3mm2,根据矩形的周长公式可得出C矩形OMON=-2m2+8m,再利用二次函数的性质即可得出当矩形PMON的周长随点P的横坐标m增大而增大时,m的取值范围.
当y=0时,有x2+3x=0,
解得:x1=0,x2=3,
∴0<m<3,
∵点P的横坐标为m,
∴点P的坐标为(m,m2+3m),OM=m,PM=3mm2,
∴C矩形OMON=2(OM+PM)=2(m+3mm2)=2m2+8m,
∴当0<m≤2时,矩形PMON的周长随点P的横坐标m增大而增大.
故答案为:0<m≤2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

-
科目: 来源: 题型:
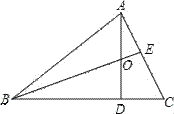
查看答案和解析>>【题目】△ABC中,AD⊥BC于点D,BE是∠ABC的平分线,已知∠ABC=40°,∠C=60°,求∠AOB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.

-
科目: 来源: 题型:
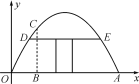
查看答案和解析>>【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为
 米.
米.(1)求该抛物线的函数关系式;
(2)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

-
科目: 来源: 题型:
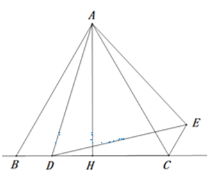
查看答案和解析>>【题目】如图,在
 中,
中,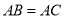 ,
, 垂足为
垂足为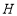 ,
,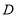 为直线
为直线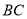 上一动点(不与点
上一动点(不与点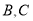 重合),在
重合),在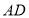 的右侧作
的右侧作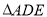 ,使得
,使得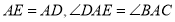 ,连接
,连接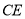 .
.(1)求证:
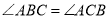 ;
;(2)当
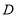 在线段
在线段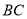 上时
上时① 求证:
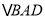 ≌
≌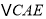 ;
; ② 若
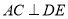 , 则
, 则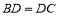 ;
;(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果)
相关试题

