【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
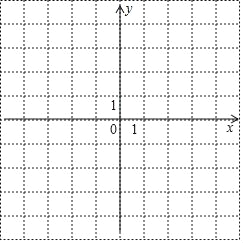
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)当
;(2)见解析;(3)当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)利用表中数据和抛物线的对称性可得到二次函数的顶点坐标为,(-1,-4),则可设顶点式y=a(x+1)-4,然后把点(1.-3)代入求出a即可;
(2)利用描点法画二次函数图象;
(3)根据x=-4,-2时的函数值即可写出y的取值范围.
(1)由题意可得二次函数的顶点坐标为![]() ,
,
设二次函数的解析式为:![]() ,
,
把点![]() 代入
代入![]() ,得
,得![]() ,
,
故抛物线解析式为![]() ,即
,即![]() ;
;
(2)如图所示:

(3)∵![]() ,
,
∴当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
又对称轴为直线![]() ,
,
∴当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
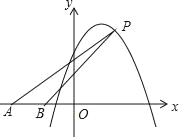
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(﹣5,0)、(﹣2,0).点P在抛物线y=﹣2x2+4x+8上,设点P的横坐标为m.当0≤m≤3时,△PAB的面积S的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)知识延伸:如图1,在
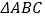 中,
中,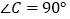 ,
, ,根据三角函数的定义得:
,根据三角函数的定义得: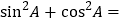 ;
;(2)拓展运用:如图2,在锐角三角形
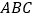 中,
中, .
.①求证:
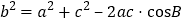 ;
;②已知:
 ,求
,求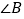 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a、b、c在数轴上的位置如图所示:

(1)用“>”、“=”或“<”填空:︱b︱ ︱c︱;—a c.
(2)化简:|b-c|-|b-a|+|a+c|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车一天下午某时间段以广场为出发点,在东西方向的大道上营运,规定向东为正,向西为负,单次行车里程依先后顺序记录如下:(单位:
 )+9,-3,-5,+4,-8,+7,-2,-5,+8,-4
)+9,-3,-5,+4,-8,+7,-2,-5,+8,-4(1)该出租车司机将最后一名乘客送到目的地后,出租车在广场的什么方向?距广场多远?
(2)若每千米耗油0.08升,该出租车这个时间段共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在圆⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
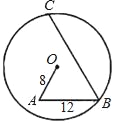
A. 19 B. 16 C. 18 D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
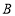 是线段
是线段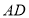 上一动点,沿
上一动点,沿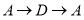 以
以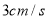 的速度往返运动1次,
的速度往返运动1次,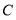 是线段
是线段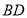 的中点,
的中点,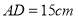 ,设点
,设点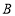 运动时间为
运动时间为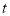 秒
秒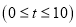 .
.
(1)当
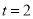 时,求线段
时,求线段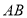 和
和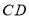 的长度.
的长度.(2)用含
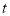 的代数式表示运动过程中
的代数式表示运动过程中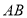 的长.
的长.(3)在运动过程中,若
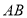 中点为
中点为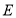 ,则
,则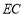 的长是否变化?若不变.求出
的长是否变化?若不变.求出 的长;若发生变化,请说明理由.
的长;若发生变化,请说明理由.
相关试题

