【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标.
参考答案:
【答案】(1)![]() ;(2)d=5+t;(3)F
;(2)d=5+t;(3)F![]() .
.
【解析】
试题分析:(1)直接把A、B坐标代入求出a、c得值即可;(2)分别过P、F向y轴作垂线,垂足分别为A′、B′,过P作PN⊥x轴,垂足为N,易证△PEA′≌△EFB′,可得出d=FM=OE﹣EB′,再代入可求得解析式;(3)先求得F、H的坐标,发现点P和点H的纵坐标相等,则PH与x轴平行,根据平行线截线段成比例定理可得G也是PQ的中点,由此表示出点G的坐标并列式,求出t的值并取舍,计算出点F的坐标.
试题解析:(1)由题意得![]() ,解得
,解得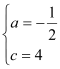 ,∴抛物线解析式为
,∴抛物线解析式为![]() ;(2)分别过P、F向y轴作垂线,垂足分别为A′、B′,过P作PN⊥x轴,垂足为N,当x=0时,y=5,∴E(0,5),∴OE=5,∵∠PEO+∠OEF=90°,∠PEO+∠EPA′=90°,∴∠EPA′=∠OEF,∵PE=EF,∠EA′P=∠EB′F=90°,∴△PEA′≌△EFB′,∴PA′=EB′=﹣t,∴d=FM=OB′=OE﹣EB′=5﹣(﹣t)=5+t;
;(2)分别过P、F向y轴作垂线,垂足分别为A′、B′,过P作PN⊥x轴,垂足为N,当x=0时,y=5,∴E(0,5),∴OE=5,∵∠PEO+∠OEF=90°,∠PEO+∠EPA′=90°,∴∠EPA′=∠OEF,∵PE=EF,∠EA′P=∠EB′F=90°,∴△PEA′≌△EFB′,∴PA′=EB′=﹣t,∴d=FM=OB′=OE﹣EB′=5﹣(﹣t)=5+t;
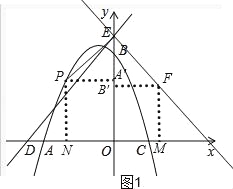
(3)如图,由直线DE的解析式为:y=x+5,∵EH⊥ED,∴直线EH的解析式为:y=﹣x+5,
∴FB′=A′E=5﹣(﹣![]() t2﹣t+4)=
t2﹣t+4)=![]() t2+t+1,∴F(
t2+t+1,∴F(![]() t2+t+1,5+t),∴点H的横坐标为:
t2+t+1,5+t),∴点H的横坐标为:![]() t2+t+1,
t2+t+1,
y=﹣![]() t2﹣t﹣1+5=﹣
t2﹣t﹣1+5=﹣![]() t2﹣t+4,∴H(
t2﹣t+4,∴H(![]() t2+t+1,﹣
t2+t+1,﹣![]() t2﹣t+4),∵G是DH的中点,∴G(
t2﹣t+4),∵G是DH的中点,∴G(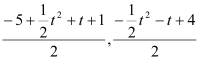 ),即G(
),即G(![]() t2+
t2+![]() t﹣2,﹣
t﹣2,﹣![]() t2﹣
t2﹣![]() t+2),∴PH∥x轴,∵DG=GH,∴PG=GQ,
t+2),∴PH∥x轴,∵DG=GH,∴PG=GQ,
∴![]() ,解得t=
,解得t=![]() ,∵P在第二象限,∴t<0,∴t=
,∵P在第二象限,∴t<0,∴t=![]() ,∴F(
,∴F(![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是方程11﹣2x=ax﹣1的解,则a=
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等式3×□﹣2×□=15的两个方格内分别填入一个数,使这两个数是互为相反数且等式成立.则第一个方格内的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一等腰三角形的周长为20,其中一边长为5,则它的腰长等于______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B是反比例函数y=
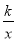 (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )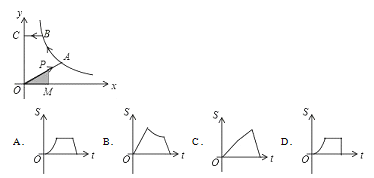
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果长方形ABCD的中心与平面直角坐标系的原点重合,且点A和点B的坐标分别为(-2,3)和(2,3),则矩形ABCD的面积为( )
A. 32 B. 24 C. 16 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家发明了一个魔术盒,当任意“数对”(a,b)进入其中时,会得到一个新的数:a2﹣b+1,例如把(3,﹣2)放入其中,就会得到32﹣(﹣2)+1=12,现将“数对”(﹣3,﹣2)放入其中后,得到的数是 .
相关试题

