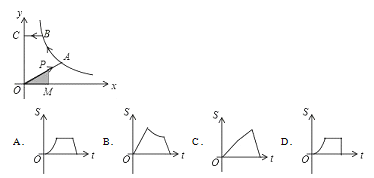
【题目】如图,已知A,B是反比例函数y=![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
参考答案:
【答案】A.
【解析】
试题分析::设∠AOM=α,点P运动的速度为a,当点P从点O运动到点A的过程中,S=![]() =
=![]() a2cosαsinαt2,由于α及a均为常量,从而可知图象本段应为抛物线,且S随着t的增大而增大;当点P从A运动到B时,由反比例函数性质可知△OPM的面积为
a2cosαsinαt2,由于α及a均为常量,从而可知图象本段应为抛物线,且S随着t的增大而增大;当点P从A运动到B时,由反比例函数性质可知△OPM的面积为![]() k,保持不变,故本段图象应为与横轴平行的线段;当点P从B运动到C过程中,OM的长在减少,△OPM的高与在B点时相同,故本段图象应该为一段下降的线段;故答案选A.
k,保持不变,故本段图象应为与横轴平行的线段;当点P从B运动到C过程中,OM的长在减少,△OPM的高与在B点时相同,故本段图象应该为一段下降的线段;故答案选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等式3×□﹣2×□=15的两个方格内分别填入一个数,使这两个数是互为相反数且等式成立.则第一个方格内的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一等腰三角形的周长为20,其中一边长为5,则它的腰长等于______.
-
科目: 来源: 题型:
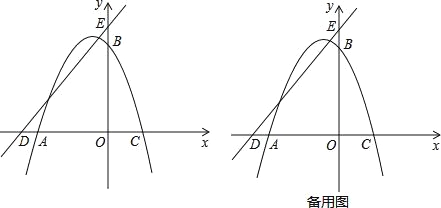
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果长方形ABCD的中心与平面直角坐标系的原点重合,且点A和点B的坐标分别为(-2,3)和(2,3),则矩形ABCD的面积为( )
A. 32 B. 24 C. 16 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家发明了一个魔术盒,当任意“数对”(a,b)进入其中时,会得到一个新的数:a2﹣b+1,例如把(3,﹣2)放入其中,就会得到32﹣(﹣2)+1=12,现将“数对”(﹣3,﹣2)放入其中后,得到的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个角是70°,则它的一个底角的度数是( )
A. 70° B. 70°或55° C. 80° D. 55°
相关试题

