【题目】如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.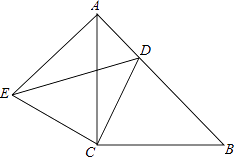
(1)求证:△BCD≌△ACE;
(2)若AE=12,DE=15,求AB的长度.
参考答案:
【答案】
(1)证明:∵△ACB与△ECD都是等腰直角三角形,
∴CE=CD,AC=BC,∠ACB=∠ECD=90°,∠B=∠BAC=45°,
∴∠ACE=∠BCD=90°﹣∠ACD,
在△ACE和△BCD中,
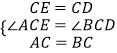 ,
,
∴△BCD≌△ACE(SAS)
(2)解:∵△BCD≌△ACE,
∴BD=AE=12,∠EAC=∠B=45°,
∴∠EAD=45°+45°=90°,
在Rt△EAD中,由勾股定理得:AD= ![]() =
= ![]() =9,
=9,
∴AB=BD+AD=12+9=21.
【解析】(1)利用等腰直角三角形的性质得出CE=CD,AC=BC,∠ACB=∠ECD=90°,∠B=∠BAC=45°,根据等式的性质得出∠ACE=∠BCD=90°﹣∠ACD,然后利用SAS判断出△BCD≌△ACE;(2)由全等三角形的性质得BD=AE=12,∠EAC=∠B=45°进而得出∠EAD=45°+45°=90°,在Rt△EAD中,由勾股定理得AD的长度,进而得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE是△ACD的角平分线,B在DA延长线上,AE∥BC,F为BC中点,判断AE与AF的位置关系并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=
 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 (x>0)的图象交于A(m,6),B(n,3)两点.
(x>0)的图象交于A(m,6),B(n,3)两点. 
(1)求一次函数的解析式;
(2)根据图象直接写出kx+6﹣ >0时,x的取值范围;
>0时,x的取值范围;
(3)若M是x轴上一点,S△MOB=S△AOB , 求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒作为奖品,请你根据图中所给的信息,解答下列问题;
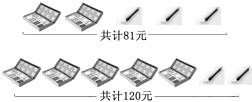
(1)求出每个颜料盒,每支水笔各多少元?
(2)若学校计划购买颜料盒和水笔共20个,所用费用不超过340元,则颜料盒至多购买多少个?
(3)恰逢商店举行优惠促销活动,具体办法如下:颜料盒按七折优惠,水笔10支以上超出部分按八折优惠,若学校决定购买同种数量的同一奖品,并且该奖品的数量超过10件,请你帮助分析,购买颜料盒合算还是购买水笔合算. -
科目: 来源: 题型:
查看答案和解析>>【题目】A城有某种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36台,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.
(1)设A城运往C乡该农机x台,运送全部农机的总费用为W元,求W关于x的函数关系式,并写出自变量x的取值范围.
(2)现该运输公司要求运送全部农机的总费用不低于16460元,则有多少种不同的调运方案?将这些方案设计出来.
(3)现该运输公司决定对A城运往C乡的农机,从运输费中每台减免a元(a≤200)作为优惠,其他费用不变,如何调运,使总费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据问题填空:
(1)问题发现:
如图①,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为;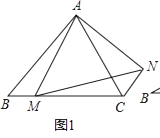
(2)深入探究:
如图②,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;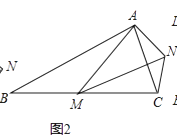
(3)拓展延伸:
如图③,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=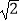 ,试求EF的长.
,试求EF的长.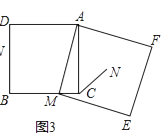
相关试题

