搜索
【题目】如图，AE是△ACD的角平分线，B在DA延长线上，AE∥BC，F为BC中点，判断AE与AF的位置关系并证明.
参考答案：
【答案】AE与AF的位置关系是垂直. 证明见解析.
【解析】
由角平分线的性质和平行线的性质得到∠B=∠ACB，由等角对等边，得到AB=AC，再由等腰三角形三线合一的性质及角平分线的性质即可得到结论．
AE与AF的位置关系是垂直．理由如下：
∵AE是△ACD的角平分线，∴∠DAE=∠CAE=
∠DAC．
∵AE∥BC，∴∠DAE=∠B，∠EAC=∠ACB，∴∠B=∠ACB，∴AB=AC．
又∵F为BC中点，∴∠BAF= ∠CAF= ∠CAB．
∵∠CAB+∠CAD=180°，∴∠CAF+∠CAE=90°，∴AE⊥AF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】列方程解应用题：
港珠澳大桥是世界上最长的跨海大桥，是被誉为“现代世界七大奇迹”的超级工程，它是我国从桥梁大国走向桥梁强国的里程碑之作．开通后从香港到珠海的车程由原来的180千米缩短到50千米，港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米，若开通后按设计时速行驶，行驶完全程时间仅为原来路程行驶完全程时间的
，求港珠澳大桥的设计时速是多少． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：|1﹣
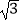|+3tan30°﹣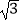（ ﹣5）0﹣（﹣ 
）﹣1 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】细观察，找规律
下列各图中的MA1与NAn平行．
（1）图①中的∠A1+∠A2= ______ 度，
图②中的∠A1+∠A2+∠A3= ______ 度，
图③中的∠A1+∠A2+∠A3+∠A4= ______ 度，
图④中的∠A1+∠A2+∠A3+∠A4+∠A5= ______ 度，
…，
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11= ______ 度
（2）第n个图中的∠A1+∠A2+∠A3+…+∠An+1= ______
（3）请你证明图②的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，长方形OABC的边OA在数轴上，O为原点，长方形OABC的面积为12，OC边长为3.
(1)数轴上点A表示的数为________．
(2)将长方形OABC沿数轴水平移动，移动后的长方形记为O′A′B′C′，移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时，数轴上点A′表示的数是多少？
②设点A的移动距离AA′＝x.
（ⅰ)当S＝4时，求x的值；
（ⅱ)D为线段AA′的中点，点E在线段OO′上，且OE＝
OO′，当点D，E所表示的数互为相反数时，求x的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b与反比例函数y=
（x＞0）的图象交于A（m，6），B（n，3）两点． 
（1）求一次函数的解析式；
（2）根据图象直接写出kx+6﹣ ＞0时，x的取值范围；
（3）若M是x轴上一点，S△MOB=S△AOB ， 求点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点．
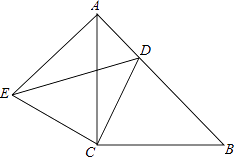
（1）求证：△BCD≌△ACE；
（2）若AE=12，DE=15，求AB的长度．
相关试题
