【题目】由于换季,一家服装店的老板想将某服装打折销售,于是她和正在上七年级的儿子商量打折方案,下面是她和儿子商量时的对话情景:
妈妈:“儿子,每件衣服按标价的5折出售,可以吗?”
儿子:“若每件衣服按标价的5折出售会亏本30元.”
妈妈:“那每件衣服按标价的8折出售呢?”
儿子:“若每件衣服按标价的8折出售将会赚60元.”
……
请根据上面的信息,解决问题:
(1)求这种服装的标价.
(2)若要不亏本,至少打几折?
参考答案:
【答案】(1)这种衣服的标价为300元.(2)要不亏本,至少打6折.
【解析】试题(1)这种服装的标价为x元,根据服装的进价不变结合进价=标价×折扣+亏损钱数(或-赚取钱数)即可得出关于x的一元一次方程,解之即可得出结论;
(2)将标价代入0.5x+30中求出这种服装的进价,再根据折扣=进价÷标价×10即可得出结论.
试题解析:
(1)设这种服装的标价为x元.
根据题意,可列方程为:
0.5x+30=0.8x-60
解之得:x=300
答:这种衣服的标价为300元.
(2)要不亏本,至少打y折.
0.5x+30=0.5×300+30=180
根据题意,可列方程为:300×![]() =180
=180
解之得:y=6
答:要不亏本,至少打6折.
-
科目: 来源: 题型:
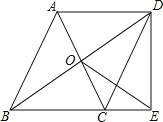
查看答案和解析>>【题目】已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.
(1)求证:DE⊥BE;
(2)设CD与OE交于点F,若OF2+FD2=OE2,CE=3,DE=4,求线段CF的长.
-
科目: 来源: 题型:
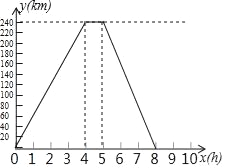
查看答案和解析>>【题目】一辆货车从A地运货到240km的B地,卸货后返回A地,如图中实线是货车离A地的路程y(km)关于出发后的时间x(h)之间的函数图象.货车出发时,正有一个自行车骑行团在AB之间,距A地40km处,以每小时20km的速度奔向B地.
(1)货车去B地的速度是 ,卸货用了 小时,返回的速度是 ;
(2)求出自行车骑行团距A地的路程y(km)关于x的函数关系式,并在此坐标系中画出它的图象;
(3)求自行车骑行团与货车迎面相遇,是货车出发后几小时后,自行车骑行团还有多远到达B地.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足
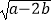 +|b﹣2|=0.
+|b﹣2|=0.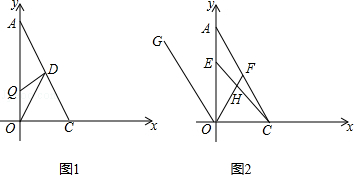
(1)则C点的坐标为;A点的坐标为 .
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.AC的中点D的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ?若存在,请求出t的值;若不存在,请说明理由
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,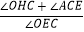 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2017的坐标为( )
A.(504,﹣504)
B.(﹣504,504)
C.(﹣504,503)
D.(﹣505,504) -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
(1)在“十一”期间,小明等同学随家长共15人到游乐园游玩,成人门票每张50元,学生门票是6折优惠.他们购票共花了650元,求一共去了几个家长、几个学生?
(2)甲、乙两人骑自行车同时从相距65千米的两地出发相向而行,甲的速度是每小时17.5千米,乙的速度是每小时15千米,求经过几小时甲、乙两人相距32.5千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3).
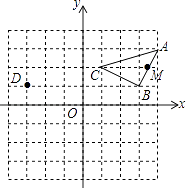
(1)点B和点C的坐标分别是、 .
(2)将△ABC平移后使点C与点D重合,点A、B与点E、F重合,画出△DEF.
并直接写出E、F的坐标.
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为 .
相关试题

