【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
参考答案:
【答案】(1)该方程有两个实数根;
(2)等腰三角形的周长为7或8,面积为![]() 或2
或2![]() .
.
【解析】分析:(1)根据方程的系数结合根的判别式,可得出△=(2k-3)2≥0,由此即可得出该方程有两个实数根;
(2)分3为底边长及腰长两种情况考虑:①当3为底边长是,由△=0可求出k值,将其代入原方程可求出三角形的腰长,再根据周长及面积公式可求出等腰三角形的周长及面积;②当3为腰长时,将x=3代入原方程可求出k值,代入k值可求出等腰三角形的底边长度,再根据周长及面积公式可求出等腰三角形的周长及面积.综上即可得出结论.
详解:(1)∵△=[-(2k+1)]2-4×4(k-![]() )=4k2-12k+9=(2k-3)2≥0,
)=4k2-12k+9=(2k-3)2≥0,
∴该方程有两个实数根;
(2)①当3为底边长时,△=(2k-3)2=0,
∴k=![]() ,
,
此时原方程为x2-4x+4=0,
解得:x1=x2=2.
∵2、2、3能组成三角形,
∴三角形的周长为2+2+3=7,三角形的面积为![]() ×3×
×3×![]()
=![]() ;
;
②当3为腰长时,将x=3代入原方程,得:9-3×(2k+1)+4(k-![]() )=0,
)=0,
解得:k=2,
此时原方程为x2-5x+6=0,
解得:x1=2,x2=3.
∵2、3、3能组成三角形,
∴三角形的周长为2+3+3=8,三角形的面积为![]() ×2×
×2×![]() .
.
综上所述:等腰三角形的周长为7或8,面积为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店因换季将某种服装打折销售,如果每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元.
问:(1)每件服装的标价、成本各是多少元?
(2)为了保证不亏损,最多可以打几折?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
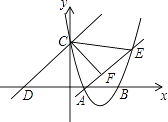
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为4的正△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB﹣BC运动,到点C停止.过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5.5秒时,PD的长是( )
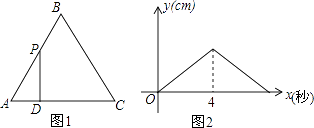
A.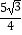 cm
cm
B.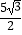 cm
cm
C.2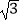 cm
cm
D.3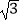 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程
 ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个反比例函数y=
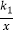 和y=
和y= 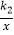 在第一象限内的图象依次是C1和C2 , 设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
在第一象限内的图象依次是C1和C2 , 设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( ) 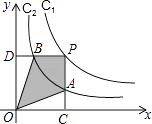
A.k1+k2
B.k1﹣k2
C.k1k2
D.k1k2﹣k2 -
科目: 来源: 题型:
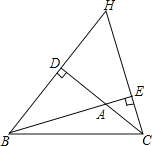
查看答案和解析>>【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)如图,①在图中找出与∠DBA相等的角,并说明理由;
②若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中,∠A=50°,直接写出∠DHE的度数是 .
相关试题

