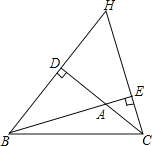
【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)如图,①在图中找出与∠DBA相等的角,并说明理由;
②若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中,∠A=50°,直接写出∠DHE的度数是 .
参考答案:
【答案】(1)①∠DBA=∠ECA,证明见解析;②80°;(2)50°或130°.
【解析】试题分析:(1)①根据同角的余角的相等即可说明∠DBA=∠ECA,根据四边形的内角和是360°,求得∠DHE的度数;
(2)分△ABC是锐角三角形,钝角三角形两种情况讨论求解即可.
(1)①∠DBA=∠ECA.
证明:∵BD、CE是△ABC的两条高,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠BAD=∠ECA+∠EAC=90°,
又∵∠BAD=∠EAC,
∴∠DBA=∠ECA;
②∵BD、CE是△ABC的两条高
∴∠HDA=∠HEA=90°
在四边形ADHE中,∠DAE+∠HDA+∠DHE+∠HEA=360°
又∵∠HDA=∠HEA=90°,∠DAE=∠BAC=100°
∴∠DHE=360°-90°-90°-100°=80°
(2)①△ABC是锐角三角形时,∠DHE=180°-50°=130°;
②△ABC是钝角三角形时,∠DHE=∠A=50°;
故答案为:50°或130°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣
 )=0.
)=0.(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程
 ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个反比例函数y=
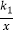 和y=
和y= 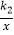 在第一象限内的图象依次是C1和C2 , 设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
在第一象限内的图象依次是C1和C2 , 设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( ) 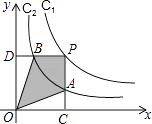
A.k1+k2
B.k1﹣k2
C.k1k2
D.k1k2﹣k2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B是数轴上的两个点,点A表示的数为13,点B表示的数为-5,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为
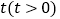 秒.
秒.(1)BP= ,点P表示的数 (分别用含
 的代数式表示);
的代数式表示);(2)点P运动多少秒时,PB=2PA?
(3)若M为BP的中点,N为PA的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
-
科目: 来源: 题型:
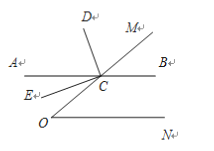
查看答案和解析>>【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
相关试题

