搜索
【题目】如图所示，两个反比例函数y= 
和y= 
在第一象限内的图象依次是C1和C2 ， 设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，则四边形PAOB的面积为（ ）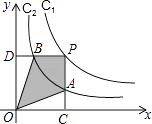 
A.k1+k2
B.k1﹣k2
C.k1k2
D.k1k2﹣k2
参考答案：
【答案】B
【解析】解：∵PC⊥x轴，PD⊥y轴， ∴S矩形PCOD=k1 ， S△AOC=S△BOD= 
×k2 ，
∴四边形PAOB的面积=S矩形PCOD﹣S△AOC﹣S△BOD=k1﹣ k2﹣ k2=k1﹣k2 ．
故选B．
【考点精析】根据题目的已知条件，利用比例系数k的几何意义的相关知识可以得到问题的答案，需要掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在边长为4的正△ABC中，点P以每秒1cm的速度从点A出发，沿折线AB﹣BC运动，到点C停止．过点P作PD⊥AC，垂足为D，PD的长度y（cm）与点P的运动时间x（秒）的函数图象如图2所示．当点P运动5.5秒时，PD的长是（ ）
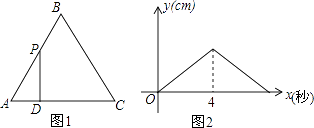
A.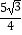
cm
B.
cm
C.2
cm
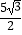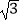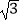D.3 cm -
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣（2k+1）x+4（k﹣
）=0．（1）判断这个一元二次方程的根的情况；
（2）若等腰三角形的一边长为3，另两条边的长恰好是这个方程的两个根，求这个等腰三角形的周长及面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道，为尽量减少施工对交通造成的影响，实施施工时“…”，设实际每天铺设管道x米，则可得方程
，根据此情景，题中用“…”表示的缺失的条件应补为（ ）
A.每天比原计划多铺设10米，结果延期15天才完成
B.每天比原计划少铺设10米，结果延期15天才完成
C.每天比原计划多铺设10米，结果提前15天才完成
D.每天比原计划少铺设10米，结果提前15天才完成 -
科目： 来源： 题型：
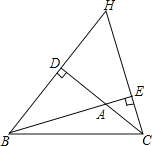
查看答案和解析>>【题目】已知BD、CE是△ABC的两条高，直线BD、CE相交于点H．
（1）如图，①在图中找出与∠DBA相等的角，并说明理由；
②若∠BAC=100°，求∠DHE的度数；
（2）若△ABC中，∠A=50°，直接写出∠DHE的度数是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知A、B是数轴上的两个点，点A表示的数为13，点B表示的数为－5，动点P从点B出发，以每秒4个单位长度的速度沿数轴向右匀速运动，设运动时间为
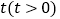秒．（1）BP= ，点P表示的数 （分别用含
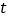的代数式表示）；（2）点P运动多少秒时，PB=2PA？
（3）若M为BP的中点，N为PA的中点，点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着柴静纪录片《穹顶之下》的播出，全社会对空气污染问题越来越重视，空气净化器的销量也大增，商社电器从厂家购进了A，B两种型号的空气净化器，已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元，用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同．
（1）求一台A型空气净化器和一台B型空气净化器的进价各为多少元？
（2）在销售过程中，A型空气净化器因为净化能力强，噪音小而更受消费者的欢迎．为了增大B型空气净化器的销量，商社电器决定对B型空气净化器进行降价销售，经市场调查，当B型空气净化器的售价为1800元时，每天可卖出4台，在此基础上，售价每降低50元，每天将多售出1台，如果每天商社电器销售B型空气净化器的利润为3200元，请问商社电器应将B型空气净化器的售价定为多少元？
相关试题
