【题目】如图,已知△ABC 的顶点分别为 A(-2,2)、B(-4,5)、C(-5,1)和直线 m (直线 m 上各点的横坐标都为 1).
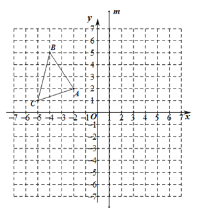
(1)作出△ABC 关于 ![]() 轴对称的图形△A1B1C1,并写出点 A1 的坐标;
轴对称的图形△A1B1C1,并写出点 A1 的坐标;
(2)作出点 C关于直线 m 对称的点C2 , 并写出点C2 的坐标;
(3)在![]() 轴上找一点P,使 PA+PC的值最小,请直接写出点P的坐标.
轴上找一点P,使 PA+PC的值最小,请直接写出点P的坐标.
参考答案:
【答案】(1)图详见解析,A1的坐标为(-2,-2);(2)图详见解析,C2(7,1);(3)图详见解析,P(-4,0)
【解析】
(1)分别作出点A,B,C关于x轴的对称点A1,B1,C1,再首尾顺次连接可得;
(2)C点坐标为(-5,1),直线m的横坐标为1,所以点C到直线m的距离为6,即点C2到直线m的距离为6,所以C2(7,1);
(3)连结AC1,与x轴的交点即为点P,写出点P坐标即可.
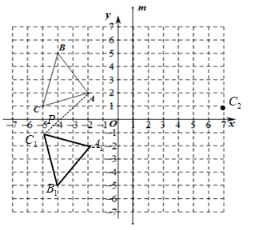
解:(1)如图所示,△A1B1C1即为所求,其中点A1的坐标为(-2,-2);
(2) 点C2如图,C2(7,1);
(3)如图所示,连结AC1,点P为所求,P(-4,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在矩形纸片
,在矩形纸片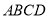 中,
中, ,
,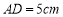 ,折叠纸片使
,折叠纸片使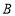 点落在边
点落在边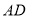 上的
上的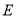 处,折痕为
处,折痕为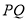 .过点
.过点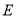 作
作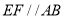 交
交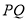 于
于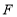 ,连接
,连接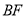 .
.(1)求证:四边形
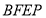 为菱形;
为菱形;(2)当点
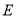 在
在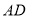 边上移动时,折痕的端点
边上移动时,折痕的端点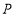 ,
,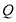 也随之移动.
也随之移动.①当点
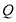 与点
与点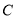 重合时(如图
重合时(如图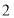 ),求菱形
),求菱形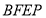 的边长;
的边长;②若限定
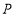 ,
,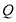 分别在边
分别在边 ,
, 上移动,求出点
上移动,求出点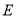 在边
在边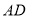 上移动的最大距离.
上移动的最大距离.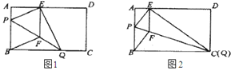
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
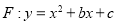 的图象经过坐标原点
的图象经过坐标原点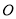 ,且与
,且与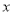 轴另交点为
轴另交点为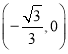 .
.(1)求抛物线
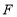 的解析式;
的解析式;(2)如图
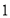 ,直线
,直线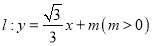 与抛物线
与抛物线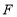 相交于点
相交于点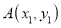 和点
和点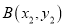 (点
(点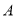 在第二象限),求
在第二象限),求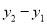 的值(用含
的值(用含 的式子表示);
的式子表示);(3)在(2)中,若
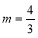 ,设点
,设点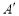 是点
是点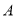 关于原点
关于原点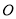 的对称点,如图
的对称点,如图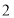 .平面内是否存在点
.平面内是否存在点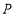 ,使得以点
,使得以点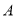 、
、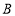 、
、 、
、 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.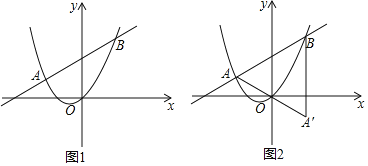
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =
 ,④
,④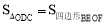 中,正确的有( )
中,正确的有( )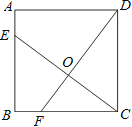
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平.为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
移动支付方式
支付宝
微信
其他
人数/人
200
75
请你根据上述统计表和统计图提供的信息.完成下列问题:
(1)在此次调查中,使用支付宝支付的人数;
(2)求表示微信支付的扇形所对的圆心角度数;
(3)某天该步行街人流量为10万人,其中30%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中,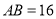 ,
, ,点
,点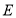 、
、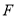 分别在边
分别在边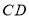 、
、 上.
上.(1)若
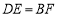 ,求证:四边形
,求证:四边形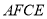 是平行四边形;
是平行四边形;(2)若四边形
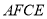 是菱形,求菱形
是菱形,求菱形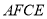 的周长.
的周长.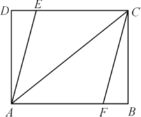
相关试题

