【题目】在数轴上有A、B两点,所表示的数分别为n,n+6,A点以每秒5个单位长度的速度向右运动,同时B点以每秒3个单位长度的速度也向右运动,设运动时间为t 秒.
(1)当n=1时,求AB的值;
(2)当t 为何值时,A、B两点重合;
(3)在上述运动的过程中,若P为线段AB的中点,数轴上点C所表示的数为n+10是否存在t 的值,使得线段PC=4,若存在,求t 的值;若不存在,请说明理由.
参考答案:
【答案】(1)|2t﹣6|;(2)当t 为3时,A、B两点重合;(3)存在t的值,使得线段PC=4,此时t的值为![]() 或
或![]() .
.
【解析】
找出运动时间为t秒时,点A、B表示的数.
(1)将n=1代入点A、B表示的数中,再根据两点间的距离公式即可得出结论;
(2)根据点A、B重合即可得出关于t的一元一次方程,解之即可得出结论;
(3)根据点A、B表示的数结合点P为线段AB的中点即可找出点P表示的数,根据PC=4即可得出关于t的一元一次方程,解之即可得出结论.
解:当运动时间为t 秒时,点A表示的数为5t+n,点B表示的数为3t+n+6.
(1)当n=1时,点A表示的数为5t+1,点B表示的数为3t+7,
AB=|5t+1﹣(3t+7)|=|2t﹣6|.
故答案为:|2t﹣6|.
(2)根据题意得:5t+n=3t+n+6,
解得:t=3.
∴当t 为3时,A、B两点重合.
(3)∵P为线段AB的中点,
∴点P表示的数为(5t+n+3t+n+6)÷2=4t+n+3,
∵PC=4,
∴|4t+n+3﹣n﹣10|=|4t﹣7|=4,
解得:t=![]() 或t=
或t=![]() .
.
∴存在t的值,使得线段PC=4,此时t的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
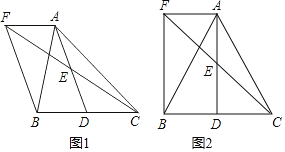
查看答案和解析>>【题目】如图1,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:点D是线段BC的中点;
(2)如图2,若AB=AC=13,AF=BD=5,求四边形AFBD的面积.
-
科目: 来源: 题型:
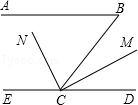
查看答案和解析>>【题目】如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于;(在横线上填上答案即可).
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,求∠OCA度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
每人加工件数
540
450
300
240
210
120
人数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数。
(2)若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额,你认为这个定额是否合理,为什么?
-
科目: 来源: 题型:
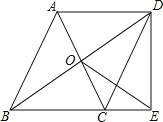
查看答案和解析>>【题目】已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.
(1)求证:DE⊥BE;
(2)设CD与OE交于点F,若OF2+FD2=OE2,CE=3,DE=4,求线段CF的长.
-
科目: 来源: 题型:
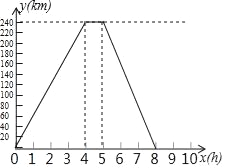
查看答案和解析>>【题目】一辆货车从A地运货到240km的B地,卸货后返回A地,如图中实线是货车离A地的路程y(km)关于出发后的时间x(h)之间的函数图象.货车出发时,正有一个自行车骑行团在AB之间,距A地40km处,以每小时20km的速度奔向B地.
(1)货车去B地的速度是 ,卸货用了 小时,返回的速度是 ;
(2)求出自行车骑行团距A地的路程y(km)关于x的函数关系式,并在此坐标系中画出它的图象;
(3)求自行车骑行团与货车迎面相遇,是货车出发后几小时后,自行车骑行团还有多远到达B地.
相关试题

