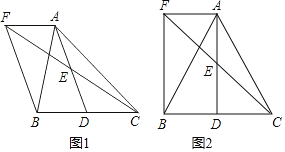
【题目】如图1,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:点D是线段BC的中点;
(2)如图2,若AB=AC=13,AF=BD=5,求四边形AFBD的面积.
参考答案:
【答案】(1)证明见解析(2)60
【解析】
(1)利用“AAS”可证明△EAF≌△EDC,则AF=DC,从而得到BD=DC;(2)先证明四边形AFBD是平行四边形,再利用等腰三角形的性质证明AD⊥BC,则四边形AFBD为矩形,然后计算出AD后再计算四边形AFBD的面积.
(1)证明:如图1,∵点E是AD的中点,
∴AE=DE,∵AF∥BC,∴∠AFE=∠DCE,∠FAE=∠CDE.
在△EAF和△EDC
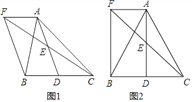
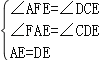 ,∴△EAF≌△EDC,∴AF=DC,∵AF=BD,
,∴△EAF≌△EDC,∴AF=DC,∵AF=BD,
∴BD=DC,即D是BC的中点;
(2)解:如图2,∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,
∵AB=AC,又由(1)可知D是BC的中点,∴AD⊥BC,
在Rt△ABD中,AD=![]() =12,∴矩形AFBD的面积=BDAD=60.
=12,∴矩形AFBD的面积=BDAD=60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】合作探究:你了解吗?骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,观察图象回答下列问题:
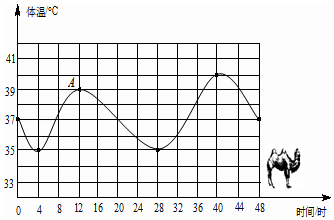
(1)一天中,骆驼的体温的变化范围是 , 它的体温从最低上升到最高需要时.
(2)从16时到24时,骆驼的体温下降了度.
(3)从时到时,骆驼的体温在上升,从时到时,从 时到时骆驼的体温在下降.
(4)你能看出第二天8时骆驼的体温与第一天8时的体温的关系是 .
(5)A点表示的是 , 还有时的温度与A点所表示的温度相同? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,

(1)写出△ABC各点的坐标.A( , )B( , )C( , ).
(2)若把△ABC向上平移1个单位,再向右平移3个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标.A′( , )B′( , )C′( , ).
(3)连结CA′,CB′,则△CA′B′的面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

-
科目: 来源: 题型:
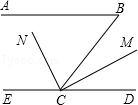
查看答案和解析>>【题目】如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于;(在横线上填上答案即可).
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,求∠OCA度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有A、B两点,所表示的数分别为n,n+6,A点以每秒5个单位长度的速度向右运动,同时B点以每秒3个单位长度的速度也向右运动,设运动时间为t 秒.
(1)当n=1时,求AB的值;
(2)当t 为何值时,A、B两点重合;
(3)在上述运动的过程中,若P为线段AB的中点,数轴上点C所表示的数为n+10是否存在t 的值,使得线段PC=4,若存在,求t 的值;若不存在,请说明理由.
相关试题

