【题目】综合与实践
问题情境
在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,且交直线
,且交直线![]() 于点
于点![]() .
.



(1)如图1,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.
自主探究
(2)如图2,当点![]() 在线段
在线段![]() 上时,其它条件不变,请猜想
上时,其它条件不变,请猜想![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
拓展延伸
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
参考答案:
【答案】(1)证明见解析;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() .
.
【解析】
(1)根据等腰直角三角形的性质得到∠A=∠ABC,根据同角的余角相等得到∠CBG=∠ACE,根据ASA公理证明△ACE≌△CBG;
(2)同理即可证明△ACE≌△CBG;
(3)CG=AE.
解:(1)在Rt△ABC中,
∵AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,
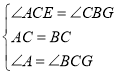 ,
,
∴△ACE≌△CBG;
(2)结论仍然成立,即△ACE≌△CBG.
理由如下:在Rt△ABC中,
∵AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
∴△ACE≌△CBG;
(3)CG=AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①三点确定一个圆;②平分弦的直径必垂直于这条弦;③圆周角等于圆心角的一半;④等弧所对的圆心角相等;⑤各角相等的圆内接多边形是正多边形.其中正确的有( )
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,完成相应任务:



(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是 命题(填“真”或“假”).
(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.
(3)小颖经过探究又提出了一个新的命题:“若
 ,
, ,
, , , ,则四边形
, , ,则四边形 ≌四边形
≌四边形 ”请在横线上填写两个关于“角”的条件,使该命题为真命题.
”请在横线上填写两个关于“角”的条件,使该命题为真命题. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是某公园为迎接“中国–南亚博览会”设置的一休闲区.
 ,弧
,弧 的半径
的半径 长是
长是 米,
米, 是
是 的中点,点
的中点,点 在弧
在弧 上,
上, ,则图中休闲区(阴影部分)的面积是( )
,则图中休闲区(阴影部分)的面积是( )
A.
 米
米 B.
B. 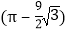 米
米 C.
C.  米
米 D.
D.  米
米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的半径是
的半径是 ,直线
,直线 与
与 相交于
相交于 、
、 两点.
两点. 是
是 上的一个动点,若
上的一个动点,若 ,则
,则 面积的最大值是________.
面积的最大值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是
是 的直径,
的直径, 是
是 的弦,弦
的弦,弦 于点
于点 ,交
,交 于点
于点 ,过点
,过点 的直线与
的直线与 的延长线交于点
的延长线交于点 ,
, .
.
 求证:
求证: 是
是 的切线;
的切线; 当点
当点 在劣弧
在劣弧 上运动时,其他条件不变,若
上运动时,其他条件不变,若 .求证:点
.求证:点 是
是 的中点;
的中点; 在满足
在满足 的条件下,
的条件下, ,
, ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:几个全等的正多边形依次有一边重合,排成一圈,中间可以围成一个正多边形,我们称作正多边形的环状连接。如图,我们可以看作正六边形的环状连接,中间围成一个边长相等的正六边形;若正八边形作环状连接,中间可以围的正多边形的边数为;

若正八边形作环状连接,中间可以围的正多边形的边数为________,若边长为1的正n边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为_________.
相关试题

