【题目】在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )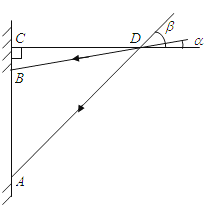
A.1.2米
B.1.5米
C.1.9米
D.2.5米
参考答案:
【答案】B
【解析】设CD为x , 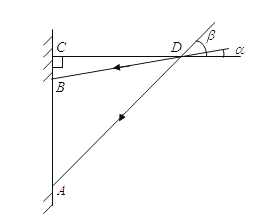
在Rt△BCD中,∠BDC=α=18°,
∵tan∠BDC= ![]() ,
,
∴BC=CDtan∠BDC=0.32x ,
在Rt△ACD中,∠ADC=β=66°,
∵tan∠ADC= ![]() ,
,
∴AC=CDtan∠ADC=2.2x ,
∵AB=AC-BC ,
∴2.82=2.2x-0.32x ,
解得:x=1.5 .
答:CD长约为1.5米 .
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,小敏.小颖分别画了△ABC和△DEF , 尺寸如图 . 如果两个三角形的面积分别记作S△ABC.S△DEF , 那么它们的大小关系是( )

A.S△ABC>S△DEF
B.S△ABC<S△DEF
C.S△ABC=S△DEF
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A.B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E , 再从E沿着垂直于AE的方向走到F , C为AE上一点,其中3位同学分别测得三组数据:①AC , ∠ACB;②EF.DE.AD;③CD , ∠ACB , ∠ADB.其中能根据所测数据求得A.B两树距离的有( )

A.0组
B.一组
C.二组
D.三组 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC , 支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( ) (栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 . 车辆尺寸:长×宽×高)
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3
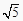 米,坡顶有旗杆BC , 旗杆顶端B点与A点有一条彩带相连 . 若AB=10米,则旗杆BC的高度为( )
米,坡顶有旗杆BC , 旗杆顶端B点与A点有一条彩带相连 . 若AB=10米,则旗杆BC的高度为( )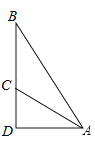
A.5米
B.6米
C.8米
D.(3+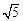 )米
)米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为∠BAC的平分线,添加下列条件后,不能证明△ABD≌△ACD的是( )

A. ∠B=∠C B. ∠BDA=∠CDA C. BD=CD D. AB=AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米 . 求放水后水面上升的高度是( )
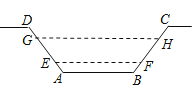
A.0.55
B.0.8
C.0.6
D.0.75
相关试题

