【题目】《函数的图象与性质》拓展学习片段展示: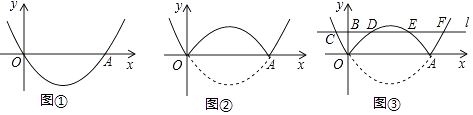
(1)【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣ ![]() 经过原点O,与x轴的另一个交点为A,则a= .
经过原点O,与x轴的另一个交点为A,则a= .
(2)【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.
(3)【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.
(4)【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.
参考答案:
【答案】
(1)![]()
(2)解:如图①,抛物线:y= ![]() (x﹣2)2﹣
(x﹣2)2﹣ ![]() ,
,
对称轴是:直线x=2,由对称性得:A(4,0),
沿x轴折叠后所得抛物线为:y=﹣ ![]() (x﹣2)2+
(x﹣2)2+ ![]()
如图②,图象G对应的函数解析式为:y= 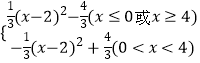 ;
;
(3)解:如图③,由题意得:
当y=1时, ![]() (x﹣2)2﹣
(x﹣2)2﹣ ![]() =1,
=1,
解得:x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ,
,
∴C(2﹣ ![]() ,1),F(2+
,1),F(2+ ![]() ,1),
,1),
当y=1时,﹣ ![]() (x﹣2)2+
(x﹣2)2+ ![]() =1,
=1,
解得:x1=3,x2=1,
∴D(1,1),E(3,1),
由图象得:图象G在直线l上方的部分,当1<x<2或x>2+ ![]() 时,函数y随x增大而增大;
时,函数y随x增大而增大;
(4)解:∵D(1,1),E(3,1),
∴DE=3﹣1=2,
∵S△PDE= ![]() DEh≥1,
DEh≥1,
∴h≥1;
①当P在C的左侧或F的右侧部分时,设P[m, ![]() ],
],
∴h= ![]() (m﹣2)2﹣
(m﹣2)2﹣ ![]() ﹣1≥1,
﹣1≥1,
(m﹣2)2≥10,
m﹣2≥ ![]() 或m﹣2≤﹣
或m﹣2≤﹣ ![]() ,
,
m≥2+ ![]() 或m≤2﹣
或m≤2﹣ ![]() ,
,
②如图③,作对称轴交抛物线G于H,交直线CD于M,交x轴于N,
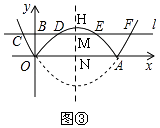
∵H(2, ![]() ),
),
∴HM= ![]() ﹣1=
﹣1= ![]() <1,
<1,
∴点P不可能在DE的上方;
③∵MN=1,
且O(0,0),A(4,0),
∴P不可能在CO(除O点)、OD、EA(除A点)、AF上,
∴P与O或A重合时,符合条件,
∴m=0或m=4;
综上所述,△PDE的面积不小于1时,m的取值范围是:m=0或m=4或m≤2﹣ ![]() 或m≥2+
或m≥2+ ![]() .
.
【解析】(1)把原点(0,0)代入解析式即可求出a的值,
∵抛物线y=a(x﹣2)2﹣ ![]() 经过原点O,
经过原点O,
∴0=a(0﹣2)2﹣ ![]() ,
,
a= ![]() ,
,
所以答案是: ![]() ;
;
(2)在0<x<4内翻折函数与点的关于x轴对称类似,横坐标x不变,纵坐标y 变为它的相反数,即-y=![]() ,y=
,y=![]() ;然后分段写出函数关系式;(3)数形结合,观察出自左到右上升的图像对应的x范围即为函数y随x增大而增大的x范围;(4)通过面积不小于1,转化为不等式:S△PDE=
;然后分段写出函数关系式;(3)数形结合,观察出自左到右上升的图像对应的x范围即为函数y随x增大而增大的x范围;(4)通过面积不小于1,转化为不等式:S△PDE= ![]() DEh≥1,∴h≥1;h为P到DE的距离,经过分析可知,P在原点或在C左侧的抛物线上或F的右侧抛物线上,解不等式即可求出.
DEh≥1,∴h≥1;h为P到DE的距离,经过分析可知,P在原点或在C左侧的抛物线上或F的右侧抛物线上,解不等式即可求出.
【考点精析】利用二次函数图象的平移对题目进行判断即可得到答案,需要熟知平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出直线y=
 x-1的图象,利用图象求:
x-1的图象,利用图象求:(1)当x≥2时,y的取值范围;
(2)当y<0时,x的取值范围;
(3)当-1≤y≤2时,对应x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步普及我市中小学生的法律知识,提升学生法律意识,在2018年12月4日第五个国家宪法日来临之际,我市某区在中小学举行了“学习宪法”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得优胜奖的学生共400名,请结合图中信息,解答下列问题:
(1)求获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场法律知识抢答赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c在数轴上的位置如图所示,回答下列问题:
(1)化简:3|a﹣c|﹣2|﹣a﹣b|;
(2)令y=|x﹣a|+|x﹣b|+|x﹣c|,x满足什么条件时,y有最小值,求最小值

-
科目: 来源: 题型:
查看答案和解析>>【题目】A地某厂和B地某厂同时制成机器若干台,A地某厂可支援外地10台,B地某厂可支援外地4台,现决定给C地8台,D地6台.已知从A运往D、C两地的运费分别是200元每台、400元每台,从B运往D、C两地的运费分别是150元每台、250元每台.
(1)设B地某厂运往D地x台,求总运费为多少元?
(2)在(1)中,当x=2时,总运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在□ABCD中,点E,F分别在边BC和AD上,且CE=AF,
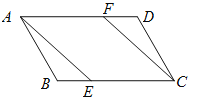
(1)求证:△ABE ≌ △CDF;
(2)求证:四边形AECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,正比例函数y=
 x的图象经过点A,点A的纵坐标为4,反比例函数y=
x的图象经过点A,点A的纵坐标为4,反比例函数y=  的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:
的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:
(1)这个反比例函数的解析式;
(2)直线AB的表达式.
相关试题

